题目内容
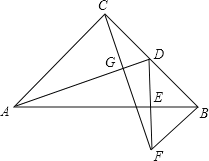
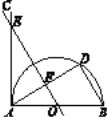
【题目】已知：如图， 
是半圆
的直径，D是半圆上的一个动点（点D不与点A，B 重合）， 
（1）求证：AC是半圆
的切线；
（2）过点O作BD的平行线，交AC于点E，交AD于点F,且EF=4, AD=6, 求BD的长．
【答案】（1）证明见解析；（2）
【解析】试题分析：（1）欲证AC是半圆O的切线，只需证明∠CAB=90°即可；
（2）由相似三角形的判定定理“两角对应相等的两个三角形相似”可以判定△AEF∽△BAD；然后根据相似三角形的对应边成比例求得BD的长即可．
（1）证明：
∵AB是半圆直径，
∴∠BDA=90°.
∴
又
∴
即∠CAB=90°
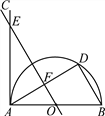
∴AC是半圆O的切线.
（2）解：由题意知，
∴∠D =∠AFO =∠AFE = 90°
∴
.
又∵AD=6
∴AF=3.
又
∴△AEF∽△BAD
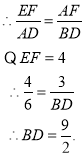
练习册系列答案
相关题目
