题目内容
【题目】已知等边![]() 和等腰
和等腰![]() ,
,![]() ,
,![]() .
.
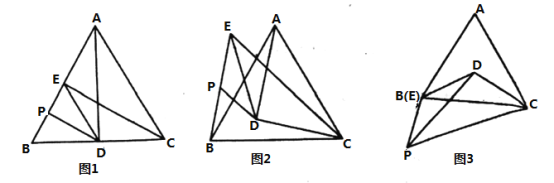
(1)如图1,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则线段
,则线段![]() 与
与![]() 之间的数量关系为 ;
之间的数量关系为 ;
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,
外部,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
(3)如图3,若点![]() 在
在![]() 内部,点
内部,点![]() 和点
和点![]() 重合,点
重合,点![]() 在
在![]() 下方,且
下方,且![]() 为定值,当
为定值,当![]() 最大时,
最大时,![]() 的度数为 .
的度数为 .
【答案】(1)![]()
![]() ;
;
(2)成立,理由见解析;
(3)![]()
【解析】
(1)根据等边三角形的性质,![]() ,
,![]() ,可得
,可得![]() 是等边三角形,
是等边三角形,![]() 是
是![]() 的中点,利用等边三角形三线合一性质,以及
的中点,利用等边三角形三线合一性质,以及![]() 得出
得出![]() ,所以PD是
,所以PD是![]() 中位线,得出点D是BC的中点,AD=CE,可得出结论
中位线,得出点D是BC的中点,AD=CE,可得出结论![]()
![]() .
.
(2)作辅助线,延长ED到F,使得![]() ,使得
,使得![]() 是等边三角形,PD是
是等边三角形,PD是![]() 的中位线,通过证明三角形全等得出
的中位线,通过证明三角形全等得出![]() 可证明结论.
可证明结论.
(3)作出等腰![]() ,由旋转模型证明三角形
,由旋转模型证明三角形![]() ,利用P、C、K三点共线时,PK最大,即PD最大可求解得.
,利用P、C、K三点共线时,PK最大,即PD最大可求解得.
(1)根据图1,在等边![]() 和等腰
和等腰![]() 中,
中,
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]()
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,![]() ,
,
![]() PD是
PD是![]() 中位线
中位线
![]() 分别是
分别是![]() 的中点,
的中点,
![]() ,
,
故答案为:![]()
![]() .
.
(2)结论成立.
理由:如下图中,延长ED到F,使得![]() ,连接FC,BF,
,连接FC,BF,
![]() ,
,
![]()
![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]() ,
,
在![]() 和
和![]() 中
中
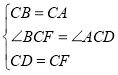
![]()
![]() ,
,
![]() ,
,
![]() ,
,
故答案为:结论成立;
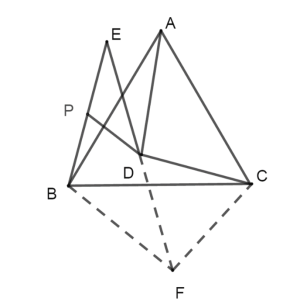
(3)作![]() ,且
,且![]() ,
,
连接PK,DK,
则![]() 为等腰三角形,
为等腰三角形,
在![]() 和
和![]() 中
中
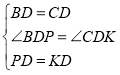
![]() ,
,
![]() ,
,
即![]() 为定值.
为定值.
P、C、K三点共线时,PK最大,即PD最大,
![]() 此时,
此时,![]() ,
,
故答案为:![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目