题目内容
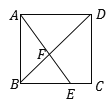
【题目】在菱形ABCD中,AE⊥BC,AF⊥CD, 且E,F分别为BC,CD的中点,求∠EAF .
【答案】60°
【解析】
首先连接AC,由四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,易得△ABC与△ACD是等边三角形,即可求得∠B=∠D=60°,继而求得∠BAD,∠BAE,∠DAF的度数,则可求得∠EAF的度数.
解:连接AC,
∵AE⊥BC,AF⊥CD,且E、F分别为BC、CD的中点,
∴AB=AC,AD=AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴AB=BC=AC,AC=CD=AD,
∴∠B=∠D=60°,
∴∠BAE=∠DAF=30°,∠BAD=180°-∠B=120°,
∴∠EAF=∠BAD-∠BAE-∠DAF=60°.

练习册系列答案
相关题目