题目内容
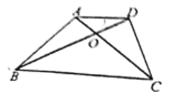
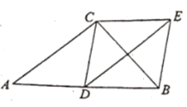
【题目】如图,已知在Rt△ABC 中,∠ACB=90°,D 是边 AB 上的中点,DE 平分∠CDB,且 DE=AC.
(1)求证:CE=AD;
(2)如果AC=BC,求证:四边形BECD 是正方形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)先证明AC∥DE,再由一组对边平行且相等即可证明四边形ACED是平行四边形,从而证明CE=AD;
(2)先证明四边形CDBE是菱形,再由等腰三角形三线合一的性质证明CD⊥BD,从而证明四边形BECD 是正方形.
(1)证明:∵∠ACB=90°,D 是边 AB 上的中点,
∴CD=AD=BD
∴∠ACD=∠A,
∴∠CDB=∠ACD+∠A=2∠A,
∵DE平分∠CDB
∴∠BDE=![]() ,
,
∴∠A=∠BDE,
∴AC∥DE,
又∵DE=AC,
∴四边形ACED是平行四边形,
∴CE=AD
(2)证明:由(1)可得,四边形ACED是平行四边形,
∴CE∥AD,CE=AD,
∵AD=BD=CD
∴CE=BD=CD
∴四边形CDBE是菱形,
又∵AC=BC,点D是AB中点,
∴CD⊥BD
∴菱形CDBE是正方形.

练习册系列答案
相关题目