题目内容
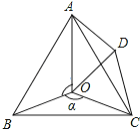
【题目】如图，点
是等边
内一点，
，
．以
为一边作等边三角形
，连接
、
．
（1）若
，判断
_______
(填“
，
或
”)
（2）当
，试判断
的形状，并说明理由；
（3）探究：当
______时，是等腰三角形．(请直接写出答案)
【答案】（1）=；（2）
是直角三角形，证明见详解；（3）
、
、
．
【解析】
（1）根据等边三角形性质得出
，利用
求出
，所以B，O，D三点共线，即有
；
（2）首先根据已知条件可以证明
，然后利用全等三角形的性质可以求出
的度数，由此即可判定
的形状；
（3）分三种情况讨论，利用已知条件及等腰三角形的性质即可求解．
解：（1）答：
证明∵
是等边三角形，
∴，
当
，即时，
，
即：B，O，D三点共线，
∴
（2）是直角三角形．
是等边三角形，
，
是等边三角形，
，
，
，
，
，
，
，
，
是直角三角形；
（3）由（2）知，
∴
，
∴
，
，
，
①要使
，需
，
，
；
②要使
，需
，
，
；
③要使
，需
，
，
．
所以，当
为、、时，是等腰三角形．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
