Question

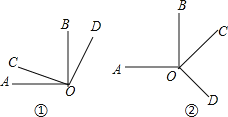
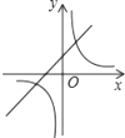
【题目】如图(1)所示，∠AOB、∠COD都是直角．

(1)试判断∠AOC与∠BOD的大小关系，并说明理由；

(2)若∠BOC=60°，求∠AOD的度数；

(3)猜想∠AOD与∠BOC在数量上是相等，互余，还是互补的关系，并说明理由；

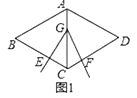
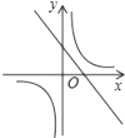
(4)当∠COD绕着点O旋转到图(2)所示位置时，你在(3)中的猜想还成立吗？请用你所学的知识加以说明．

Answer 1

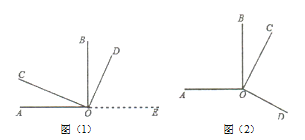
【答案】（1），理由详见解析；（2）120°；（3），理由详见解析；（4）成立，理由详见解析．

【解析】

（1）根据角的和差可以求得∠AOC、∠BOD的大小关系．

（2）根据角的和差求出∠AOC和∠AOD的度数即可；

（3）根据直角的定义可得∠AOB=∠COD=90°，然后用∠AOD和∠COB表示出∠BOD，列出方程整理即可得解；

（4）根据周角等于360°列式整理即可得解．

（1）如图①，相等，理由如下：

∵∠AOB、∠COD都是直角，∴∠AOB=∠COD=90°，∴∠AOB﹣∠BOC=∠COD﹣∠BOC，即∠AOC=∠BOD；

（2）∵∠BOC=60°，∠AOB=90°，∴∠AOC=∠AOB-∠BOC =90°-60°=30°．

∵∠COD=90°，∴∠AOD=∠COD+∠AOC= 90°+30°=120°．

（3）∠AOD与∠COB互补．理由如下：

∵∠AOB、∠COD都是直角，∴∠AOB=∠COD=90°，∴∠BOD=∠AOD﹣∠AOB=∠AOD﹣90°，∠BOD=∠COD﹣∠COB=90°﹣∠COB，∴∠AOD﹣90°=90°﹣∠COB，∴∠AOD+∠COB=180°，∴∠AOD与∠COB互补；

（4）成立．理由如下：

∵∠AOB、∠COD都是直角，∴∠AOB=∠COD=90°．

∵∠AOB+∠BOC+∠COD+∠AOD=360°，∴∠AOD+∠COB=180°，∴∠AOD与∠COB互补．