题目内容
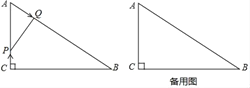
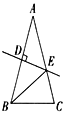
【题目】如图，等腰三角形ABC的底角为72°，腰AB的垂直平分线交另一腰AC于点E，垂足为D，连接BE,则下列结论错误的是（ ）
A. ∠EBC为36° B. BC = AE
C. 图中有2个等腰三角形 D. DE平分∠AEB
【答案】C
【解析】
根据等腰三角形的性质和线段垂直平分线的性质一一判断即可．
A．∵等腰△ABC的底角为72°，∴∠A＝180°﹣72°×2＝36°．
∵AB的垂直平分线DE交AC于点E，∴AE＝BE，∴∠ABE＝∠A＝36°，∴∠EBC＝∠ABC﹣∠ABE＝36°．故A正确；
B．∵∠ABE＝∠A＝36°，∴∠BEC=72°．
∵∠C=72°，∴∠BEC=∠C，∴BE=BC．
∵AE=BE，∴BC=AE，故B正确；
C．∵BC=BE=AE，∴△BEC、△ABE是等腰三角形．
∵△ABC是等腰三角形，故一共有3个等腰三角形，故C错误；
D．∵AE＝BE，DE⊥AB，∴DE平分∠AEB．故D正确．
故选C．
练习册系列答案
名校课堂系列答案
相关题目
