题目内容
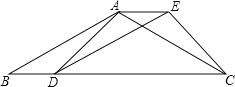
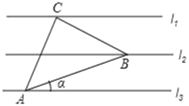
【题目】如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
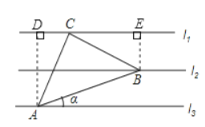
过点A作AD⊥l1于D,过点B作BE⊥l1于E,根据同角的余角相等求出∠CAD=∠BCE,然后利用“角角边”证明△ACD和△CBE全等,根据全等三角形对应边相等可得CD=BE,然后利用勾股定理列式求出AC,再根据等腰直角三角形斜边等于直角边的![]() 倍求出AB,然后利用锐角的正弦等于对边比斜边列式计算即可得解.
倍求出AB,然后利用锐角的正弦等于对边比斜边列式计算即可得解.
解:如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,设l1,l2,l3间的距离为1,
∵∠CAD+∠ACD=90°,
∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在等腰直角△ABC中,AC=BC,
在△ACD和△CBE中,∠CAD=∠BCE,∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS),
∴CD=BE=1,
在Rt△ACD中,AC=![]()
在等腰直角△ABC中,AB=![]() AC=
AC=![]() ,
,
∴sinα=![]() .
.
故选:D.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目