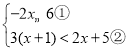��Ŀ����
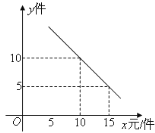
����Ŀ��ij�ľ����۵����������г�ѡ��A��B�����ľߣ�������A��Ϊ12Ԫ/����B��Ϊ8Ԫ/�������õ�����A��B�����ľߵ���������y�����������ۼ�x��Ԫ/��������һ�κ�����ϵ������ͼ��
��1����y��x�ĺ�����ϵʽ��
��2���õ�ƻ����ѡ��A��B�����ľߵ�������120���������ʽ���1200Ԫ����ϣ��ȫ���������������178Ԫ������A���ľ���������6����B���ľ�ÿ���ɻ���1Ԫ���㣬��õ�������ļ��ֽ���������
��3����A���ľߵ����ۼ۱�B���ľߵ����ۼ۸�4Ԫ/�����������ľ�ÿ�����������Ԫ����A���ľ����ۼ�x��Ԫ/����֮��ĺ�����ϵʽ����˵��A��B�����ľ����ۼ۷ֱ�Ϊ����ʱ��ÿ�����۵��������
���𰸡���1��![]() ����2�������ֽ����������ֱ�������
����2�������ֽ����������ֱ�������![]() ��58����
��58����![]() ��62��������
��62��������![]() ��59����
��59����![]() ��61��������
��61��������![]() ��60����
��60����![]() ��60������3��
��60������3��![]() ��
��![]() �ľ����ۼ�Ϊ16Ԫ��
�ľ����ۼ�Ϊ16Ԫ��![]() �ľ����ۼ�Ϊ12Ԫʱ�������
�ľ����ۼ�Ϊ12Ԫʱ�������
��������
��1���ô���ϵ���������ʽ��
��2�����������![]() ���ľ�
���ľ�![]() ���������������ȡֵ��Χ�����ʵ�����ȡ��������⣻
���������������ȡֵ��Χ�����ʵ�����ȡ��������⣻
��3������A���ľߵ����ۼ۱�B���ľߵ����ۼ۸�4Ԫ/����A���ľ����ۼ�x��Ԫ/��������B���ľ����ۼۣ�x-4����Ԫ/������ÿ��A���ľߵ�����Ϊ��x-12��Ԫ��ÿ��B���ľߵ�����Ϊ��x-4-8��Ԫ���ݴ��г����̣�Ȼ�ɵõ������
�⣺��1����ͼ��֪����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
��![]() ����������ã�
����������ã�![]() ��
��
���![]() ��
��
![]() ��
��
��2����![]() ʱ����
ʱ����![]() ����
����![]() ���ۼ�Ϊ14Ԫ��
���ۼ�Ϊ14Ԫ��
���������![]() ���ľ�
���ľ�![]() ������
������![]() �ľ���
�ľ���![]() ���������⣬��
���������⣬��![]() ��
��
���![]() ��
��
���ľߵ�����Ϊ������
�������ֽ����������ֱ�������![]() ��58����
��58����![]() ��62��������
��62��������![]() ��59����
��59����![]() ��61��������
��61��������![]() ��60����
��60����![]() ��60����
��60����
��3����A���ľߵ����ۼ۱�B���ľߵ����ۼ۸�4Ԫ/����A���ľ����ۼ�x��Ԫ/����
��B���ľ����ۼۣ�x-4����Ԫ/������ÿ��A���ľߵ�����Ϊ��x-12��Ԫ��ÿ��B���ľߵ�����Ϊ��x-4-8��Ԫ��
�������ľ�ÿ�����������![]() ��
��
��������![]() ��
��
��![]() �������ľ�ÿ����������������ֵ����ÿ�����۵��������
�������ľ�ÿ����������������ֵ����ÿ�����۵��������
��![]() �ľ����ۼ�Ϊ16Ԫ��
�ľ����ۼ�Ϊ16Ԫ��![]() �ľ����ۼ�Ϊ12Ԫʱ�������
�ľ����ۼ�Ϊ12Ԫʱ�������

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�