题目内容
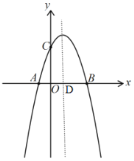
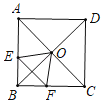
【题目】在边长为![]() 的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△OEF的面积为y,则能反映y与x之间关系的图象为( )
的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△OEF的面积为y,则能反映y与x之间关系的图象为( )
A. B.
B.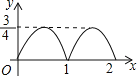
C.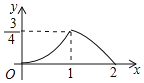 D.
D.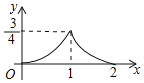
【答案】B
【解析】
分析,EF与x的关系,他们的关系分两种情况,依情况来判断抛物线的开口方向.
解:∵四边形ABCD是正方形,
∴AC=BD=![]() ,OB=OD=
,OB=OD=![]()
![]() ,
,
①当P在OB上时,即0≤x≤![]() ,
,
∵EF∥AC,
∴△BEF∽△BAC,
∴EF:AC=BP:OB,
∴EF=2BP=2x,
∴y=![]() EFOP=
EFOP=![]() ×2x
×2x![]() =
=![]() ;
;
②当P在OD上时,即![]() <x≤
<x≤![]() ,
,
∵EF∥AC,
∴△DEF∽△DAC,
∴EF:AC=DP:OD,
即EF:![]() :
:![]() ,
,
∴EF=2(![]() ﹣x),
﹣x),
∴y=![]() EFOP=
EFOP=![]() =
=![]() ,
,
这是一个二次函数,根据二次函数的性质可知:
二次函数的图象是一条抛物线,开口方向取决于二次项的系数.
当系数>0时,抛物线开口向上;系数<0时,开口向下.
根据题意可知符合题意的图象只有选项B.
故选:B.

练习册系列答案
相关题目