题目内容
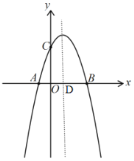
【题目】如图,二次函数![]() 的图象与x轴交于A,B两点,与y轴交于点C,对称轴与x轴交于点D,若点P为y轴上的一个动点,连接PD,则
的图象与x轴交于A,B两点,与y轴交于点C,对称轴与x轴交于点D,若点P为y轴上的一个动点,连接PD,则![]() 的最小值为________.
的最小值为________.
【答案】![]()
【解析】
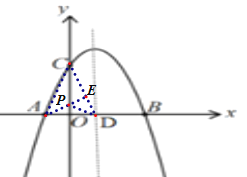
连接AC,连接CD,过点A作AE⊥CD交于点E,则AE为所求.由锐角三角函数的知识可知![]() PC=PE,然后通过证明△CDO∽△AED,利用相似三角形的性质求解即可.
PC=PE,然后通过证明△CDO∽△AED,利用相似三角形的性质求解即可.
解:连接AC,连接CD,过点A作AE⊥CD交于点E,则AE为所求.
当x=0时,y=3,
∴C(0,3).
当y=0时,
0=-x2+2x+3,
∴x1=3,x2=-1,
∴A(-1,0)、B(3,0),
∴OA=1,OC=3,
∴AC=![]() ,
,
∵二次函数y=-x2+2x+3的对称轴是直线x=1,
∴D(1,0),
∴点A与点D关于y轴对称,
∴sin∠ACO=![]() ,
,
由对称性可知,∠ACO=∠OCD,PA=PD,CD= AC=![]() ,
,
∴sin∠OCD=![]() ,
,
∵sin∠OCD=![]() ,
,
∴![]() PC=PE,
PC=PE,
∵PA=PD,
∴![]() PC+PD=PE+PA,
PC+PD=PE+PA,
∵∠CDO=∠ADE, ∠COD=AED,
∴△CDO∽△AED,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
故答案为![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目