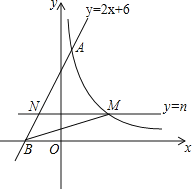Question

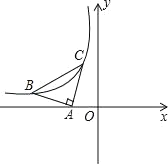
【题目】如图，已知点A的坐标为（﹣1，0），且AB＝AC＝，∠BAC＝90°，若B、C均在反比例函数y＝的图象上，则k＝_____．

Answer 1

【答案】﹣

【解析】

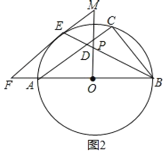
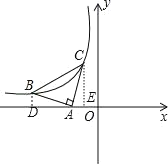
作BD⊥x轴于D，CE⊥x轴于E，如图先证明△ABD≌△ACO得到AE=BD，CE=AD，设C（a，b），则CO=b，AE=a+1，则可表示出B点坐标为（-b-1，a+1），
再根据反比例函数图象上点的坐标特征得到k=ab=（-b-1）（a+1），根据勾股定理得到（a+1）2+b2=（）2，然后解关于a、b的方程组，根据-1＜a＜0，b＞0确定a、b的值，然后计算ab即可．

解：作BD⊥x轴于D，CE⊥x轴于E，如图，

∵∠BAC＝90°，

∴∠CAE+∠BAD＝90°，

∵∠CAE+∠ACO＝90°，

∴∠BAD＝∠ACO，

在△ABD和△ACO中，

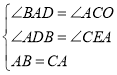
∴△ABD≌△ACO，

∴AE＝BD，CE＝AD，

设C（a，b），则CO＝b，AE＝a+1，

∴BD＝a+1，AD＝b，

∴B点坐标为（﹣b﹣1，a+1），

∵点C和点B在反比例函数y＝的图象上，

∴k＝ab＝（﹣b﹣1）（a+1），

在Rt△ACE中，∵AE2+CE2＝AC2，

∴（a+1）2+b2＝（）2，

解得a＝﹣2﹣，b＝1﹣（舍去）或a＝﹣2，b＝1+或a＝（1﹣），b＝（﹣3﹣）（舍去）或a＝（1+），b＝（﹣3）（舍去），

∴k＝ab＝（﹣2）（1+）＝﹣．

故答案为﹣．