题目内容
已知:在矩形ABCD中,AB=6cm,AD=9cm,点P从点B出发,沿射线BC方向以每秒2cm的速度移动,同时,点Q从点D出发,沿线段DA以每秒1cm的速度向点A方向移动(当点Q到达点A时,点P与点Q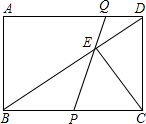 同时停止移动),PQ交BD于点E.假设点P移动的时间为x(秒),△BPE的面积为y(cm2).
同时停止移动),PQ交BD于点E.假设点P移动的时间为x(秒),△BPE的面积为y(cm2).
(1)求证:在点P、Q的移动过程中,线段BE的长度保持不变;
(2)求y关于x的函数解析式,并写出它的定义域;
(3)如果CE=CP,求x的值.
 同时停止移动),PQ交BD于点E.假设点P移动的时间为x(秒),△BPE的面积为y(cm2).
同时停止移动),PQ交BD于点E.假设点P移动的时间为x(秒),△BPE的面积为y(cm2).(1)求证:在点P、Q的移动过程中,线段BE的长度保持不变;
(2)求y关于x的函数解析式,并写出它的定义域;
(3)如果CE=CP,求x的值.
(1)证明:∵DQ∥BP,
∴
=
.(1分)
∵BP=2x,DQ=x,
∴
=2.
∴BE=
BD.(1分)
∵∠A=90°,AB=6,AD=9,
∴BD=3
.(1分)
∴BE=2
,
即在点P和点Q的移动过程中,线段BE的长度保持不变.(1分)
(2)作EH⊥BC,垂足为点H,得EH∥CD.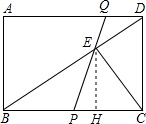
∴
=
=
.(1分)
∴EH=4.(1分)
∴y=
•2x•4,
即所求的函数解析式为y=4x.(1分)
定义域为0<x≤9.(1分)
(3)∵EH∥CD,
∴
=
=
.
∴CH=3.(1分)
∴CE=5.(1分)
(i)当点P在线段BC上时,9-2x=5.解得x=2.(1分)
(ii)当点P在线段BC的延长线上时,2x-9=5.解得x=7.(1分)
∴
| BE |
| DE |
| BP |
| DQ |
∵BP=2x,DQ=x,
∴
| BE |
| DE |
∴BE=
| 2 |
| 3 |
∵∠A=90°,AB=6,AD=9,
∴BD=3
| 13 |
∴BE=2
| 13 |
即在点P和点Q的移动过程中,线段BE的长度保持不变.(1分)
(2)作EH⊥BC,垂足为点H,得EH∥CD.

∴
| EH |
| DC |
| BE |
| BD |
| 2 |
| 3 |
∴EH=4.(1分)
∴y=
| 1 |
| 2 |
即所求的函数解析式为y=4x.(1分)
定义域为0<x≤9.(1分)
(3)∵EH∥CD,
∴
| CH |
| BC |
| DE |
| BD |
| 1 |
| 3 |
∴CH=3.(1分)
∴CE=5.(1分)
(i)当点P在线段BC上时,9-2x=5.解得x=2.(1分)
(ii)当点P在线段BC的延长线上时,2x-9=5.解得x=7.(1分)

练习册系列答案
相关题目
 ,且AB∶
,且AB∶ =1∶2 ,已知BC=8,则
=1∶2 ,已知BC=8,则 的长是( )
的长是( )