题目内容
在△ABC中AB=AC，AD为高，点E在AC上，BE交AD于F，EC：AE=1：3，则FD：AF=______．
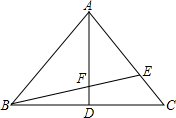
如图，过点E作EG∥BC交AD于G，
∵EC：AE=1：3，
∴
=
=
，
∴
=
=
=
，
=
=3，
∵AB=AC，AD为高，
∴BD=CD，
∵EG∥BC，
∴
=
=
=
，
设FD=4x，则GF=3x，
∴AG=3DG=3（GF+FD）=3（3x+4x）=21x，
∴AF=AG+GF=21x+3x=24x，
∴FD：AF=4x：24x=1：6．
故答案为：1：6．
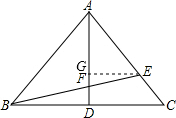
∵EC：AE=1：3，
∴
| AE |
| AC |
| 3 |
| 1+3 |
| 3 |
| 4 |
∴
| EG |
| CD |
| AG |
| AD |
| AE |
| AC |
| 3 |
| 4 |
| AG |
| DG |
| AE |
| EC |
∵AB=AC，AD为高，
∴BD=CD，
∵EG∥BC，
∴
| GF |
| FD |
| EG |
| BD |
| EG |
| CD |
| 3 |
| 4 |
设FD=4x，则GF=3x，
∴AG=3DG=3（GF+FD）=3（3x+4x）=21x，
∴AF=AG+GF=21x+3x=24x，
∴FD：AF=4x：24x=1：6．
故答案为：1：6．
练习册系列答案
相关题目
同时停止移动），PQ交BD于点E．假设点P移动的时间为x（秒），△BPE的面积为y（cm2）．
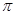米2
