题目内容
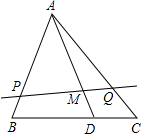
如图,AD是△ABC的中线,E是AC上任一点,BE交AD于点O,数学兴趣小组的同学在研究这个图形时,得到如下结论:
(1)当
=
时,
=
;
(2)当
=
时,
=
;
(3)当
=
时,
=
猜想,当
=
时,(n是正整数),
的一般结论,并说明理由.

(1)当
| AO |
| AD |
| 1 |
| 2 |
| AE |
| AC |
| 1 |
| 3 |
(2)当
| AO |
| AD |
| 1 |
| 3 |
| AE |
| AC |
| 1 |
| 5 |
(3)当
| AO |
| AD |
| 1 |
| 4 |
| AE |
| AC |
| 1 |
| 7 |
猜想,当
| AO |
| AD |
| 1 |
| n+1 |
| AE |
| AC |

当
=
时,(n是正整数),
=
.
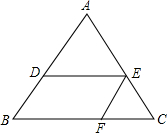
过D点作DF∥BE交AC于点F,
∵
=
,
=
,
∵AD是△ABC的中线,
∴D是BC的中点,
∵BE∥DF,
∴EF=CF,
∴
=
.
利用中位线定理即可得证.
| AO |
| AD |
| 1 |
| n+1 |
| AE |
| AC |
| 1 |
| 2n+1 |
过D点作DF∥BE交AC于点F,
∵
| AO |
| AD |
| 1 |
| n+1 |
| AE |
| AF |
| 1 |
| n+1 |
∵AD是△ABC的中线,
∴D是BC的中点,
∵BE∥DF,
∴EF=CF,
∴
| AE |
| AC |
| 1 |
| 2n+1 |
利用中位线定理即可得证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
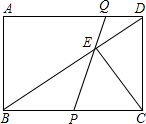 同时停止移动),PQ交BD于点E.假设点P移动的时间为x(秒),△BPE的面积为y(cm2).
同时停止移动),PQ交BD于点E.假设点P移动的时间为x(秒),△BPE的面积为y(cm2).
 米2
米2