题目内容
【题目】计算:
(1)![]()
(2)小明解不等式![]() ≤1的过程如下,请指出他解答过程中开始出现错误步骤的序号,并写出正确的解答过程.
≤1的过程如下,请指出他解答过程中开始出现错误步骤的序号,并写出正确的解答过程.
解:去分母得:3(1+x)﹣2(2x+1)≤1……①
去括号得:3+3x﹣4x+1≤1……②
移项得:3x﹣4x≤1﹣3﹣1……③
合并同类项得:﹣x≤﹣3……④
两边都除以﹣1得:x≤3……⑤
解:开始出现错误的步骤序号为 ,正确的解答过程 .
(3)已知实数x,y满足方程组![]() ,求
,求![]() 的平方根;
的平方根;
(4)求不等式组 的整数解.
的整数解.
【答案】(1)1+![]() ;(2)①,见解析;(3)±2;(4)-2,-1
;(2)①,见解析;(3)±2;(4)-2,-1
【解析】
(1)根据立方根和绝对值的性质计算即可
(2)根据一元一次不等式的解法,找出错误的步骤,并写出正确的解答过程即可.
(3)先求出方程组的解,再求出4x2y的值,再求出平方根即可.
(4)先求出不等式组的解集,再找出整数解即可
(1)原式=5-3+![]() -1=1+
-1=1+![]()
(2)开始出现错误的步骤序号为①,正确解答过程如下:
去分母,得3(1+x)2(2x+1)6,
去括号,得3+3x4x26,
移项,得3x4x63+2,
合并同类项,得x5,
两边都除以1,得x5.
(3)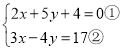
①×4+②×5得:23x=69,
解得:x=3,
把x=3代入②得:94y=17,
解得:y=2,
∴4x2y=4×32×(2)=16,![]() =4
=4
所以![]() 的平方根是±2.
的平方根是±2.
(4)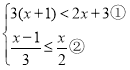 ,
,
由不等式①得x<0,
由不等式②得x≥-2,
所以不等组的解集为-2≤x<0,
则这个不等式组的整数解是-2,-1.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目