题目内容
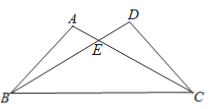
【题目】将两块全等的含![]() 角的直角三角板按图
角的直角三角板按图![]() 的方式放置,已知
的方式放置,已知![]() ,
,![]() .
.
![]() 固定三角板
固定三角板![]() ,然后将三角板
,然后将三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,
所示的位置,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
①填空:当旋转角等于![]() 时,
时,![]() ________度;
________度;
②当旋转角等于多少度时,![]() 与
与![]() 垂直?请说明理由.
垂直?请说明理由.
![]() 将图
将图![]() 中的三角板
中的三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,使
所示的位置,使![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,试说明
,试说明![]() .
.

【答案】(1)①![]() ;②当旋转角等于
;②当旋转角等于![]() 时,
时,![]() 与
与![]() 垂直,理由详见解析;(2)详见解析.
垂直,理由详见解析;(2)详见解析.
【解析】
(1)①根据旋转的性质得∠A1CA=20°,则利用互余得∠ACB1=70°,然后根据∠BCB1=∠ACB+∠ACB1进行计算;
②利用AB与A1B1垂直得∠A1ED=90°,则∠A1DE=90°-∠A1=60°,根据对顶角相等得∠BDC=60°,由于∠B=60°,利用三角形内角和定理得∠A1CB=180°-∠BDC-∠B=60°,所以∠ACA1=90°-∠A1CB=30°,然后根据旋转的定义得到旋转角等于30°时,AB与A1B1垂直;
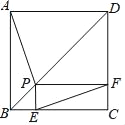
(2)由于AB∥CB1,∠ACB1=90°,根据平行线的性质得∠ADC=90°,在Rt△ADC中,根据含30度的直角三角形三边的关系得到CD=![]() AC,再根据旋转的性质得AC=A1C,所以CD=
AC,再根据旋转的性质得AC=A1C,所以CD=![]() A1C,则A1D=CD.
A1C,则A1D=CD.
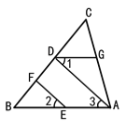
(1)①∵将三角板ABC绕点C顺时针方向旋转至图2所示的位置,
∴∠A1CA=20°
∴∠ACB1=70°,
∴∠BCB1=∠ACB+∠ACB1=160°;
故答案为160;
②当旋转角等于![]() 时,
时,![]() 与
与![]() 垂直.理由如下:
垂直.理由如下:
当![]() 与
与![]() 垂直时,
垂直时,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
即旋转角等于![]() 时,
时,![]() 与
与![]() 垂直;
垂直;
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵图![]() 中的三角板
中的三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,
所示的位置,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目