��Ŀ����
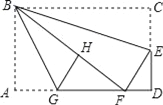
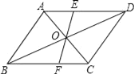
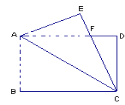
����Ŀ����֪������ABC����DEF�У���A=40������E+��F=100��������DEF��ͼ�ڷţ�ʹ�á�D�������߷ֱ���B�͵�C��
��1��������DEF��ͼ1�ڷ�ʱ�����ABD+��ACD= �ȣ�
��2��������DEF��ͼ2�ڷ�ʱ���������ABD+��ACD�Ķ�������˵�����ɣ�
��3���ܷ���DE�ڷŵ�ij��λ��ʱ��ʹ��BD��CDͬʱƽ�֡�ABC�͡�ACB��ֱ��д������ ����������������������
���𰸡���1��240����2��30�㣻��3������.
��������
��1��Ҫ���ABD+��ACD�Ķ�����ֻҪ�����ABC+��CBD+��ACB+��BCD�������������ڽǺͶ����ó���ABC+��ACB=180��-��A=180��-40��=140���������������ڽǺͶ�������CBD+��BCD=��E+��F=100�����ó���ABD+��ACD=��ABC+��CBD+��ACB+��BCD=140��+100��=240����
��2��Ҫ���ABD+��ACD�Ķ�����ֻҪ�����ABC+��ACB-����BCD+��CBD���Ķ����������������ڽǺͶ�������CBD+��BCD=��E+��F=100���������������ڽǺͶ����ã���ABC+��ACB=180��-��A=140�����ó���ABD+��ACD=��ABC+��ACB-����BCD+��CBD��=140��-100��=40����
��3�����ܣ������ܽ���DEF�ڷŵ�ij��λ��ʱ��ʹ��BD��CDͬʱƽ�֡�ABC�͡�ACB�����CBD+��BCD=��ABD+��ACD=100������ô��ABC+��ACB=200�������������ڽǺͶ���ì�ܣ����Բ��ܣ�
��1������ABC����A+��ABC+��ACB=180������A=40��
���ABC+��ACB=180��-��A=180��-40��=140��
����BCD����D+��BCD+��CBD=180��
���BCD+��CBD=180��-��D
����DEF����D+��E+��F=180��
���E+��F=180��-��D
���CBD+��BCD=��E+��F=100��
���ABD+��ACD=��ABC+��CBD+��ACB+��BCD=140��+100��=240����
�ʴ�Ϊ240��
��2����ABD+��ACD=30����
�������£�
�ߡ�E+��F=100��
���D=180��-����E+��F��=80��
���ABD+��ACD=180��-��A-��DBC-��DCB
=180��-50��-��180��-80����
=30����
��3�����ܣ������ܽ���DEF�ڷŵ�ij��λ��ʱ��ʹ��BD��CDͬʱƽ�֡�ABC�͡�ACB�����CBD+��BCD=��ABD+��ACD=100������ô��ABC+��ACB=200�������������ڽǺͶ���ì�ܣ�
�ʴ�Ϊ�����ܣ�

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�