题目内容
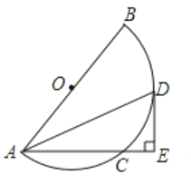
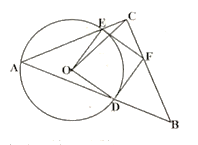
【题目】如图,等腰![]() 的一个锐角顶点
的一个锐角顶点![]() 是
是![]() 上的一个动点,
上的一个动点,![]() ,腰
,腰![]() 与斜边
与斜边![]() 分别交
分别交![]() 于点
于点![]() ,分别过点
,分别过点![]() 作
作![]() 的切线交于点
的切线交于点![]() ,且点
,且点![]() 恰好是腰
恰好是腰![]() 上的点,连接
上的点,连接![]() ,若
,若![]() 的半径为4,则
的半径为4,则![]() 的最大值为:( )
的最大值为:( )
A.![]() B.
B.![]() C.6D.8
C.6D.8
【答案】A
【解析】
先由等腰三角形的性质、切线的性质及圆的半径相等判定四边形ODFE是正方形,再得出点C在以EF为直径的半圆上运动,则当OC经过半圆圆心G时,OC的值最大,用勾股定理计算出OG的长度,再加上CG的长度即可.
解:∵等腰Rt△ABC中,∠ACB=90°,
∴∠A=∠B=45°,
∴∠DOE=2∠A=90°,
∵分别过点D,E作⊙O的切线,
∴OD⊥DF,OE⊥EF,
∴四边形ODFE是矩形,
∵OD=OE=4,
∴四边形ODFE是正方形,
∴EF=4,
∵点F恰好是腰BC上的点,
∴∠ECF=90°
∴点C在以EF为直径的半圆上运动,
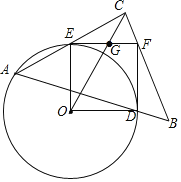
∴设EF的中点为G,则EG=FG=CG=![]() EF=2,且当OC经过半圆圆心G时,OC的值最大,此时,在Rt△OEG中,OG=
EF=2,且当OC经过半圆圆心G时,OC的值最大,此时,在Rt△OEG中,OG=![]() ,
,
∴OC=OG+CG=![]() .
.
故答案为:A.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目