Question

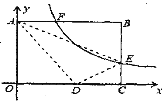
【题目】如图，将矩形ABCO放在直角坐标系中，其中顶点B的坐标为(10， 8)，E是BC边上一点将△ABE沿AE折叠，点B刚好与OC边上点D重合，过点E的反比例函数y=的图象与边AB交于点F, 则线段AF的长为( )

A. B. 2 C. D.

Answer 1

【答案】A

【解析】

首先根据翻折变换的性质，可得AD=AB=10，DE=BE；然后设点E的坐标是（10，b），在Rt△CDE中，根据勾股定理，求出CE的长度，进而求出k的值是多少；最后用k的值除以点F的纵坐标，求出线段AF的长为多少即可．

∵△ABE沿AE折叠，点B刚好与OC边上点D重合，

∴AD=AB=10，DE=BE，

∵AO=8，AD=10，

∴OD=＝6，CD=10-6=4，

设点E的坐标是（10，b），

则CE=b，DE=10-b，

∵CD2+CE2=DE2，

∴42+b2=（8-b）2，

解得b=3，

∴点E的坐标是（10，3），

∴k=10×3=30，

∴线段AF的长为：

30÷8＝．

故选：A．