题目内容
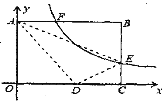
【题目】如图，ABCD中，∠DAB＝30°，AB＝6，BC＝2，P为边CD上的一动点，则2PB+ PD的最小值等于______.
【答案】
【解析】
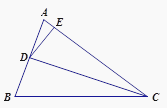
过点P作PE⊥AD交AD的延长线于点E，根据四边形ABCD是平行四边形，得到 AB∥CD，推出PE=
PD，由此得到当PB+PE最小时2PB+ PD有最小值，此时P、B、E三点在同一条直线上，利用∠DAB＝30°，∠AEP=90°，AB=6求出PB+PE的最小值=AB=3，得到2PB+ PD的最小值等于6.
过点P作PE⊥AD交AD的延长线于点E，
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠EDC=∠DAB＝30°，
∴PE=PD，
∵2PB+ PD=2（PB+PD）=2(PB+PE)，
∴当PB+PE最小时2PB+ PD有最小值，此时P、B、E三点在同一条直线上，
∵∠DAB＝30°，∠AEP=90°，AB=6，
∴PB+PE的最小值=AB=3，
∴2PB+ PD的最小值等于6，
故答案为：6.
练习册系列答案
通城学典默写能手系列答案
相关题目
