题目内容
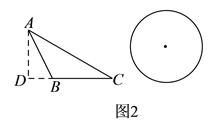
【题目】如图1,△ABC和△DBC都是边长为2的等边三角形.

(1)以图1中的某个点为旋转中心,旋转△DBC,就能使△DBC与△ABC重合,则满足题意的点为: (写出符合条件的所有点);
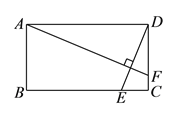
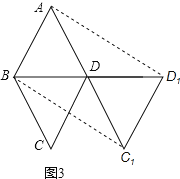
(2)将△DBC沿BC方向平移得到△D1B1C1,如图2、图3,则四边形ABD1C1是平行四边形吗?证明你的结论;
(3)在(2)的条件下,当BB1= 时,四边形ABD1C1为矩形.
【答案】(1)B点、C点、BC的中点;(2)是平行四边形.理由见解析;(3)2
【解析】
(1)根据等边三角形的性质,得到四边形ABCD是菱形,从而再根据菱形是中心对称图形,得到旋转中心有B点、C点、BC的中点;
(2)根据平移的性质,得到BB1=CC1,根据等边三角形的性质,得到AC=B1D1,∠BB1D1=∠ACC1,从而得到△BB1D1≌△ACC1,则AB=C1D1,再根据两组对边分别平行的四边形是平行四边形即可证明;
(3)根据等边三角形的性质得出AD=BD=DD1,∠ADB=60°,进而得出∠BAD=90°,再利用矩形的判定得出即可.
解:(1)∵等边△ABC和等边△DBC有公共的底边BC,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形.
∴要旋转△DBC,使△DBC与△ABC重合,有三点分别为:B点、C点、BC的中点,
故答案为:B点、C点、BC的中点;
(2)四边形ABD1C1是平行四边形.理由如下:
根据平移的性质,得到BB1=CC1,
根据等边三角形的性质,得到AC=B1D1,∠BB1D1=∠ACC1,
∴△BB1D1≌△ACC1,
∴AC1=BD1,
又AB=C1D1,
∴四边形ABD1C1是平行四边形;
(3)当移动距离BB1=2时,四边形ABC1D1是矩形.
理由:连接BC1,AD1,
∵△ABD,△BDC都是边长为2的等边三角形,
∴AD=BD=DD1,∠ADB=60°,
∴∠DAD1=∠DD1A=30°,
∴∠BAD=60°+30°=90°,
∵由(2)可得出四边形ABC1D1是平行四边形,
∴平行四边形ABC1D1是矩形.
故答案为:2.

【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t分钟,估计当![]() 时,
时,![]() 的值为( )
的值为( )
A. 140B. 200C. 240D. 260