Question

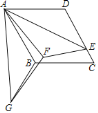
【题目】如图，在菱形ABCD中，，点E在边CD上，且，与关于AE所在的直线成对称图形以点A为中心，把顺时针旋转，得到，连接GF，则线段GF的长为______．

Answer 1

【答案】

【解析】

连接BE，作BH⊥CD于H，先证△BAE≌△FAG，得到BE=GF，在Rt△BCH中，由∠C=60°得出CH=4，BH2=48，再在Rt△BEH中，利用勾股定理即可求出BE的长即可得解.

解：如图，连接BE，作BH⊥CD于H，则∠BHC=90°，

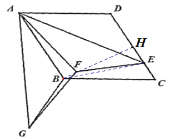
由题意可知，菱形ABCD中，AB=BC=CD=AD=8，DE=6，∠C=∠DAB，

由旋转知识可知，∠DAB=60°，AE=AG，∠DAE=∠BAG，

由对称知识可知，AD=AF，∠DAE=∠FAE，

∴∠C=∠DAB=60°，EC=CD-DE=8-6=2，AB=AF，∠FAE＝∠BAG，

∴∠FAE＋∠BAF=∠BAG+∠BAF，即∠BAE=∠FAG，

∴△BAE≌△FAG，

∴BE=GF，

∵∠BHC=90°，∠C=60°，

∴CH＝BC·cos60°=8×=4，

∴HE=CH-CE=4-2=2，BH2=BC2-CH2=82-42=48，

∴GF=BE===.

故答案为：.