题目内容
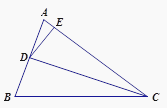
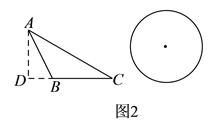
【题目】如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角两边分别交AB,AC边于M,N两点,连接MN.

(1)探究:线段BM,MN,NC之间的关系,并加以证明。
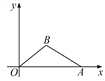
(2)若点M是AB的延长线上的一点,N是CA的延长线上的点,其它条件不变,请你再探线段BM,MN,NC之间的关系,在图②中画出图形,并说明理由。
【答案】(1)MN=BM+NC.理由见解析;(2)MN=NCBM,图见解析,理由见解析;
【解析】
(1)延长AC至E,使得CE=BM并连接DE,构造全等三角形,找到相等的线段,MD=DE,再进一步证明△DMN≌△DEN,进而得到MN=BM+NC.
(2)按要求作出图形,先证△BMD≌△CED,再证△MDN≌△EDN(SAS),即可得出结论.
(1)MN=BM+NC.理由如下:
延长AC至E,使得CE=BM(或延长AB至E,使得BE=CN),并连接DE.
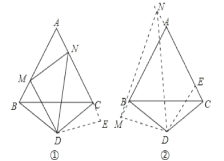
∵△BDC为等腰三角形,△ABC为等边三角形,
∴BD=CD,∠DBC=∠DCB,∠MBC=∠ACB=60°,
又BD=DC,且∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABC+∠DBC=∠ACB+∠DCB=60°+30°=90°,
∴∠MBD=∠ECD=90°,
在△MBD与△ECD中,
∵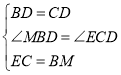 ,
,
∴△MBD≌△ECD(SAS),
∴MD=DE,
∴△DMN≌△DEN,
∴MN=BM+NC.
(2)按要求作出图形,(1)中结论不成立,应为MN=NCBM.
在CA上截取CE=BM.
∵△ABC是正三角形,
∴∠ACB=∠ABC=60°,
又∵BD=CD,∠BDC=120°,
∴∠BCD=∠CBD=30°,
∴∠MBD=∠DCE=90°,
在△BMD和△CED中
∵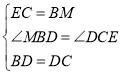 ,
,
∴△BMD≌△CED(SAS),
∴DE=DM,
在△MDN和△EDN中
∵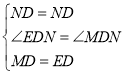 ,
,
∴△MDN≌△EDN(SAS),
∴MN=NE=NCCE=NCBM.