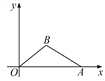
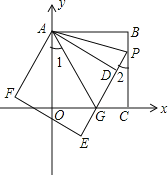
题目内容
【题目】如图,正方形![]() 的边
的边![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 坐标
坐标![]() ,将正方形
,将正方形![]() 绕点
绕点![]() 顺时针旋转角度
顺时针旋转角度![]() ,得到正方形
,得到正方形![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,
,![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,连
,连![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数,并判断线段
的度数,并判断线段![]() 、
、![]() 、
、![]() 之间的数量关系,说明理由;
之间的数量关系,说明理由;
(3)当![]() 时,求直线
时,求直线![]() 的解析式.
的解析式.

【答案】(1)见解析;(2)![]() ,
,![]() ;(3)直线
;(3)直线![]() 的解析式为
的解析式为![]() .
.
【解析】
(1)由![]() ,
,![]() ,利用“
,利用“![]() ”可证
”可证![]() ;
;
(2)利用(1)的方法,同理可证![]() ,得出
,得出![]() ,
,![]() ,而
,而![]() ,由此可求
,由此可求![]() 的度数;根据两对全等三角形的性质,可得出线段
的度数;根据两对全等三角形的性质,可得出线段![]() 、
、![]() 、
、![]() 之间的数量关系;
之间的数量关系;
(3)由![]() 可知,
可知,![]() ,而
,而![]() ,
,![]() ,当
,当![]() 时,可证
时,可证![]() ,而
,而![]() ,得出
,得出![]() ,即
,即![]() ,解直角三角形求
,解直角三角形求![]() ,
,![]() ,确定
,确定![]() 、
、![]() 两点坐标,得出直线
两点坐标,得出直线![]() 的解析式.
的解析式.
(1)证明:![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中,
![]()
![]() ,
,
![]() ;
;
(2)解:![]() .
.
由(1)同理可证![]() ,
,
则![]() ,由(1)可知,
,由(1)可知,![]() ,
,
又![]() ,
,
所以,![]() ,即
,即![]() ,
,
故![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(3)解:![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,四边形
,四边形![]() 是正方形,
是正方形,
∴![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,则
,则![]() 点坐标为:
点坐标为:![]() ,
,![]() ,
,
![]() ,在
,在![]() 中,
中,
![]() ,
,![]() ,则
,则![]() 点坐标为:
点坐标为:![]() ,
,![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以,直线![]() 的解析式为
的解析式为![]() .
.

练习册系列答案
相关题目
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t分钟,估计当![]() 时,
时,![]() 的值为( )
的值为( )
A. 140B. 200C. 240D. 260