题目内容

【题目】如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+3b），宽为（a+b）的大长方形，则需要A类、B类和C类卡片的张数分别为（　　）

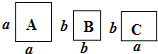
A.3，5，2B.3，7，2C.2，3，5D.2，5，7

【答案】C

【解析】

先将大长方形的面积算出为（2a+3b）×（a+b）=，由题意可知为A类卡片面积，为B类卡片面积，为C类卡片面积，则根据多项式即能求出A、B、C相应的卡片数量．

解：由题意可知，大长方形的长为（2a+3b），宽为（a+b），则其面积为（2a+3b）×（a+b）=；

由图可知，A类卡片面积为，B类卡片面积为，C类卡片面积为，由大长方形的面积多项式可知，的系数为2，的系数为3，的系数为5，则需要A类卡片2张，B类卡片3张， C类卡片5张．

故答案选：C．

练习册系列答案
相关题目

【题目】如图，抛物线经过A（﹣1，0），B（5，0），C（0，）三点．

（1）求抛物线的解析式；

（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；

（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

【题目】问题：如图①，在等边三角形ABC内有一点P，且PA＝2，PB=，PC＝1，求∠BPC的度数和等边三角形ABC的边长．

李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形(如图②)，连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形(由勾股定理的逆定理可证)，可得∠AP′B＝ °，所以∠BPC＝∠AP′B＝ °，还可证得△ABP是直角三角形，进而求出等边三角形ABC的边长为 ，问题得到解决．

（1）根据李明同学的思路填空：∠AP′B＝ °，∠BPC＝∠AP′B＝ °，等边三角形ABC的边长为 ．

（2）探究并解决下列问题：如图③，在正方形ABCD内有一点P，且PA＝，PB＝，PC＝1.求∠BPC的度数和正方形ABCD的边长．

【题目】某公司销售智能机器人，售价每台为10万元，进价y与销售量x的函数关系式如图所示。

(1)当x=10时，公司销售机器人的总利润为___万元；

(2)当10x30时，求出y与x的函数关系式；

(3)问：销售量为多少台时，公司销售机器人的总利润为37.5万元。

【题目】如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD.

（1）求证：四边形OCED为菱形；

（2）连接AE、BE，AE与BE相等吗？请说明理由.

【题目】如图，在△ABC中，∠ABC=2∠C，AP和BQ分别为∠BAC和∠ABC的角平分线，若△ABQ的周长为18，BP=4，则AB的长为_____________

【题目】已知：矩形OABC的顶点O在平面直角坐标系的原点，边OA、OC分别在x、y轴的正半轴上，且OA=3cm，OC=4cm，点M从点A出发沿AB向终点B运动，点N从点C出发沿CA向终点A运动，点M、N同时出发，且运动的速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t秒．

（1）当点N运动1秒时，求点N的坐标；(提示:过N作x轴y轴垂线，垂足分别为D,ECN:CA=CE:CO=NE:OA)

（2）试求出多边形OAMN的面积S与t的函数关系式；

（3）t为何值时，以△OAN的一边所在直线为对称轴翻折△OAN，翻折前后的两个三角形所组成的四边形为菱形？

【题目】如图，一次函数y＝﹣x+的图象与反比例函数y＝（k＞0）的图象交于A，B两点，过点A做x轴的垂线，垂足为M，△AOM面积为1．

（1）求反比例函数的解析式；并直接写出不等式的解集．

（2）在x轴上求一点P，使|PA﹣PB|的值最大，并求出其最大值和P点坐标．

（3）连接OB，求三角形AOB的面积．

【题目】若平面直角坐标系内的点 M 满足横、纵坐标都为整数，则把点 M 叫做“整点”．例如：P(1，0)、Q(2，－2)都是“整点”．抛物线 y=mx2－2mx+m－1(m>0)与 x 轴交于 A、 B 两点，若该抛物线在 A、B 之间的部分与线段 AB 所围成的区域（包括边界）恰有 6 个整点，则 m 的取值范围是( )

A. m B. m C. m D. m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网