题目内容
【题目】如图,一次函数y=﹣![]() x+
x+![]() 的图象与反比例函数y=
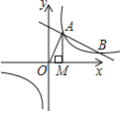
的图象与反比例函数y=![]() (k>0)的图象交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图象交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;并直接写出不等式![]() 的解集.
的解集.
(2)在x轴上求一点P,使|PA﹣PB|的值最大,并求出其最大值和P点坐标.
(3)连接OB,求三角形AOB的面积.
【答案】(1)y=![]() ,1≤x≤4或x<0;(2)P点坐标为(5,0);(3)
,1≤x≤4或x<0;(2)P点坐标为(5,0);(3)![]()
【解析】
(1)利用△AOM面积求得k的值,然后联立方程组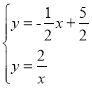 ,解此方程组,求得A、B两点坐标,利用图像,求得不等式解集;
,解此方程组,求得A、B两点坐标,利用图像,求得不等式解集;
(2)一次函数y=﹣![]() x+
x+![]() 的图象与x轴的交点即为P点,此时|PA﹣PB|的值最大,最大值为AB的长;
的图象与x轴的交点即为P点,此时|PA﹣PB|的值最大,最大值为AB的长;
(3)求出一次函数与x轴交点坐标P,利用S△AOB=S△AOP﹣S△BOP求解.
(1)∵反比例函数y=![]() (k>0)的图象过点A,过A点作x轴的垂线,垂足为M,△AOM面积为1,
(k>0)的图象过点A,过A点作x轴的垂线,垂足为M,△AOM面积为1,
∴![]() |k|=1,
|k|=1,
∵k>0,
∴k=2,
故反比例函数的解析式为:y=![]() ,
,
由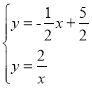 ,解得
,解得![]() 或
或![]() ,
,
∴A(1,2),B(4,![]() ),
),
由图像可知不等式![]() ≤
≤![]() 的解集为1≤x≤4或x<0;
的解集为1≤x≤4或x<0;
(2)一次函数y=![]() 的图象与x轴的交点即为P点,此时|PA﹣PB|的值最大,最大值为AB的长.
的图象与x轴的交点即为P点,此时|PA﹣PB|的值最大,最大值为AB的长.
∵A(1,2),B(4,![]() ),利用勾股定理可得
),利用勾股定理可得
∴AB=![]() ,
,
∴|PA﹣PB|的最大值为![]() ;
;
∵一次函数y=﹣![]() x+
x+![]() ,
,
令y=0,则﹣![]() x+
x+![]() =0,解得x=5,
=0,解得x=5,
∴P点坐标为(5,0);
(3)∵P(5,0),
∴OP=5,
∴S△AOB=S△AOP﹣S△BOP=![]() ×5×2﹣
×5×2﹣![]() =
=![]() .
.


练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目