Question

【题目】已知：矩形OABC的顶点O在平面直角坐标系的原点，边OA、OC分别在x、y轴的正半轴上，且OA=3cm，OC=4cm，点M从点A出发沿AB向终点B运动，点N从点C出发沿CA向终点A运动，点M、N同时出发，且运动的速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t秒．

（1）当点N运动1秒时，求点N的坐标；(提示:过N作x轴y轴垂线，垂足分别为D,ECN:CA=CE:CO=NE:OA)

（2）试求出多边形OAMN的面积S与t的函数关系式；

（3）t为何值时，以△OAN的一边所在直线为对称轴翻折△OAN，翻折前后的两个三角形所组成的四边形为菱形？

Answer 1

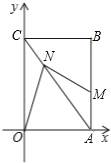
【答案】（1）N的坐标为；

（2）多边形OAMN的面积S=，（0≤t≤4）．

（3）t的值为，或．

【解析】试题分析：（1）过N作NE⊥y轴，作NF⊥x轴，由△CEN∽△COA，利用相似比求EN，再用勾股定理求CE，确定N点坐标；（2）将多边形OAMN分为△ONA和△AMN，用t分别表示两个三角形的面积，再求和即可；（3）分为①直线ON为对称轴，②直线OA为对称轴，③直线AN为对称轴，画出图形，根据菱形的特殊性，列方程求解．

试题解析：（1）∵t=1∴CN=1，AM=1

过N作NE⊥y轴，作NF⊥x轴

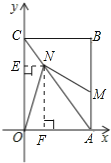
过N作NE⊥y轴，NF⊥x轴，

∴△CEN∽△COA,

∴，即，

∴EN=．

由勾股定理得：，，

∴．

（2）由（1）得，∴，

∴N点坐标为．

∵多边形OAMN由△ONA和△AMN组成

∴，，

∴多边形OAMN的面积S=（0≤t≤4）.

（3）①直线ON为对称轴时，翻折△OAN得到△OA′N，此时组成的四边形为OANA′，

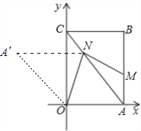
当AN=A′N=A′O=OA，四边形OANA’是菱形．

即AN=OA，∴5-t=3∴t=2．

②直线OA为对称轴时，翻折△OAN得到△OAN′，

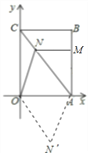
此时组成的四边形为ONAN′，连接NN′，交OA于点G．

当NN′与OA互相垂直平分时，四边形ONAN′是菱形．

即OA⊥NN′，OG=AG=，

∴NG∥CO，∴点N是AC的中点，

∴CN=，∴

③直线AN为对称轴时，翻折△OAN得到△O′AN，

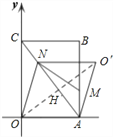
此时组成的四边形为ONO′A，连接OO’，交AN于点H．

当OO′与AN互相垂直平分时，四边形ONO’A是菱形．

即OH⊥AC，AH=NH=，

由面积法可求得OH=，

在Rt△OAH中，由勾股定理得，AH=．

∴，∴

综上所述，t的值为．