Question

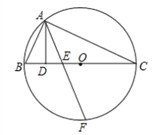
【题目】如图，△ABC内接于⊙O，且BC是⊙O的直径，AD⊥BC于D，F是弧BC中点，且AF交BC于E，连接OA，

（1）求证：AE平分∠DAO；

（2）若AB=6，AC=8，求OE的长．

Answer 1

【答案】（1）证明见解析；（2）OE=.

【解析】试题分析：（1）连接OA，由BC是 O的直径，AD⊥BC，易得∠C=∠OAE=∠B，又由F是弧BC中点，可得∠BAF=∠CAF，继而证得AE平分∠DAO；

（2）首先连接OF，易得OF∥AD，即可得DE：OE=AD：OF，然后由勾股定理求得AD，BD的长，继而求得答案．

试题解析：

（1）证明：连接OA，

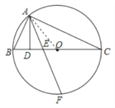
∵BC是⊙O的直径，

∴∠BAC=90°，

∴∠C+∠B=90°，

∵AD⊥BC，

∴∠B+∠BAD=90°，

∴∠BAD=∠C，

∵OA=OC，

∴∠OAC=∠C，

∴∠BAD=∠OAC，

∵F是弧BC中点，

∴∠BAF=∠CAF，

∴∠DAE=∠OAE，

即AE平分∠DAO；

（2）解：连接OF，

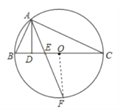
∵∠BOF=2∠BAF=∠BAC=90°，

∴OF⊥BC，

∵AD⊥BC，

∴OF∥AD，

∴DE：OE=AD：OF，

∵AB=6，AC=8，

∴BC=AB2+AC2=10，

∴AD=ABAC

BC=4.8，

∴BD=AB2AD2=3.6，

∴OD=OB-BD=5-3.6=1.4，

∴DE：OE=4.8：5=24：25，

∴OE=.