题目内容
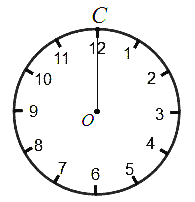
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN. 
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系;
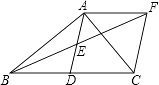
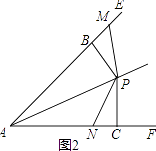
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
【答案】
(1)解:如图1,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
∵在Rt△PBM和Rt△PCN中,PBM=∠PCN=90°,
![]() ,
,
∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN
(2)AM+AN=2AC
(3)解:如图2,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
∵在Rt△PBM和Rt△PCN中,PBM=∠PCN=90°,
![]() ,
,
∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN,
∴S△PBM=S△PCN
∵AC:PC=2:1,PC=4,
∴AC=8,
∴由(2)可得,AB=AC=8,PB=PC=4,
∴S四边形ANPM=S△APN+S△APB+S△PBM
=S△APN+S△APB+S△PCN
=S△APC+S△APB
= ![]() ACPC+
ACPC+ ![]() ABPB
ABPB
= ![]() ×8×4+
×8×4+ ![]() ×8×4
×8×4
=32
【解析】解:(2)AM+AN=2AC.
∵∠APB=90°﹣∠PAB,∠APC=90°﹣∠PAC,点P为∠EAF平分线上一点,
∴∠APC=∠APB,即AP平分∠CPB,
∵PB⊥AB,PC⊥AC,
∴AB=AC,
又∵BM=CN,
∴AM+AN=(AB﹣MB)+(CN+AC)=AB+AC=2AC;
所以答案是:AM+AN=2AC.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对角平分线的性质定理的理解,了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

【题目】从![]() 开始,连续的奇数相加,它们和的情况如表所示:
开始,连续的奇数相加,它们和的情况如表所示:
加数的个数 | 连续奇数的和 |
|
|
|
|
|
|
|
|
|
|
|
|
(![]() )当
)当![]() 的值为__________.
的值为__________.
(![]() )用含
)用含![]() 的代数式表示
的代数式表示![]() 个连续奇数之和
个连续奇数之和![]() 的公式,
的公式, ![]() __________.
__________.
用含![]() 的代数式表示从
的代数式表示从![]() 开始的第
开始的第![]() 个连续奇数是__________.
个连续奇数是__________.
(![]() )根据规律计算
)根据规律计算![]() .
.
【题目】某校2015年八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
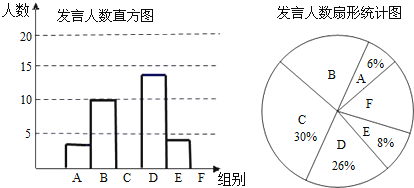
发言次数n | 人数 | 百分比 | |
A | 0≤n<3 | ||
B | 3≤n<6 | ||
C | 6≤n<9 | ||
D | 9≤n<12 | ||
E | 12≤n<15 | ||
F | 15≤n<18 |
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.