题目内容
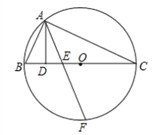
【题目】已知直线AB:y=﹣ ![]() x+5与x轴、y轴分别交于点A、B,y轴上点C的坐标为(0,10).
x+5与x轴、y轴分别交于点A、B,y轴上点C的坐标为(0,10).
(1)求A、B两点的坐标;
(2)动点M从A点出发,以每秒1个单位长度的速度,沿x轴向左运动,连接CM.设点M的运动时间为t,△COM的面积为S,求S与t的函数关系式;(并标出自变量的取值范围)
(3)直线AB与直线CM相交于点N,点P为y轴上一点,且始终保持PM+PN最短,当t为何值时,△COM≌△AOB,并求出此时点P的坐标.
【答案】
(1)
解:对于直线AB::y=﹣ ![]() x+5
x+5
当x=0时,y=5;当y=0时,x=10,
则A、B两点的坐标分别为A(10,0)、B(0,5)
(2)
解:∵C(0,10),A(10,0)
∴OC=OA=10,
当0≤t≤10时,OM=OA﹣AM=10﹣t,S△OCM= ![]() ×10×(10﹣t)=50﹣5t;
×10×(10﹣t)=50﹣5t;
当t>10时,OM=AM﹣OA=t﹣10,S△OCM= ![]() ×10×(t﹣10)=5t﹣50;
×10×(t﹣10)=5t﹣50;
∴S= ![]()
(3)
解:分为两种情况:①当M在OA上时,OB=OM=5,△COM≌△AOB.
∴AM=OA﹣OM=10﹣5=5
∴动点M从A点以每秒1个单位的速度沿x轴向左移动5个单位,所需要的时间是5秒钟;
M′(5,0),
②当M在AO的延长线上时,OM=OB=5,
则M″(﹣5,0),
∴动点M从A点以每秒1个单位的速度沿x轴向左移动15个单位,所需要的时间是15秒钟;
连接M″N交y轴于P,
∴当t为5或15时,△COM≌△AOB,
∵C(0,10),M′(5,0),
∴直线CM′为:y=﹣2x+10,
由  解得
解得  ,
,
∴N( ![]() ,
, ![]() ),
),
∵M″(﹣5,0),
∴直线M″N为y= ![]() x+2,
x+2,
∴P点的坐标为(0,2);

【解析】(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;(2)由面积公式S= ![]() ×|OM|×|OC|,求出S与t之间的函数关系式;(3)若△COM≌△AOB,OM=OB则t时间内移动了AM,可算出t值,并得到M′和M″点坐标,根据M′的坐标和C的坐标求得直线CM′的解析式,再结合直线AB
×|OM|×|OC|,求出S与t之间的函数关系式;(3)若△COM≌△AOB,OM=OB则t时间内移动了AM,可算出t值,并得到M′和M″点坐标,根据M′的坐标和C的坐标求得直线CM′的解析式,再结合直线AB
的解析式求得交点N的坐标,根据N的坐标和M″的坐标求得直线NM″的解析式,即可求得与y轴的交点P的坐标;

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
成 绩 | 45 | 46 | 47 | 48 | 49 | 50 |
人 数 | 1 | 2 | 4 | 2 | 5 | 1 |
这此测试成绩的中位数和众数分别为( )
A.47, 49
B.48, 49
C.47.5, 49
D.48, 50
【题目】某校2015年八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
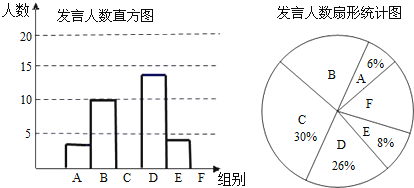
发言次数n | 人数 | 百分比 | |
A | 0≤n<3 | ||
B | 3≤n<6 | ||
C | 6≤n<9 | ||
D | 9≤n<12 | ||
E | 12≤n<15 | ||
F | 15≤n<18 |
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.