��Ŀ����
����Ŀ����֪��![]() ��
�� ![]() �������϶�Ӧ��ʵ���ֱ���
�������϶�Ӧ��ʵ���ֱ���![]() ��
�� ![]() ������
������![]() ��
�� ![]() ����
����![]() ��
��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
��![]() ����
����![]() �������϶�Ӧ����Ϊ
�������϶�Ӧ����Ϊ![]() ����
����![]() �Ƿ���
�Ƿ���![]() �Ľ⣬���������Ƿ���ڵ�
�Ľ⣬���������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������ڣ������
�������ڣ������![]() ��Ӧ�������������ڣ�˵�����ɣ�
��Ӧ�������������ڣ�˵�����ɣ�
��![]() ���ڣ�
���ڣ�![]() ���ͣ�
���ͣ�![]() ���������£���
���������£���![]() ��
�� ![]() ��
�� ![]() ͬʱ��ʼ���������˶�������
ͬʱ��ʼ���������˶�������![]() ��ÿ��
��ÿ��![]() ����λ�������ٶ������˶�����
����λ�������ٶ������˶�����![]() �͵�
�͵�![]() �ֱ���ÿ��
�ֱ���ÿ��![]() ����λ���Ⱥ�
����λ���Ⱥ�![]() ����λ���ȵ��ٶ������˶�����
����λ���ȵ��ٶ������˶�����![]() ���
���![]() ֮������ʾΪ
֮������ʾΪ![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() �����˶�ʱ��Ϊ
�����˶�ʱ��Ϊ![]() �룬��̽��������ʱ��
�룬��̽��������ʱ��![]() �ı仯��
�ı仯�� ![]() ��
��![]() ����������������ϵ����д����Ӧ�ĵ�ʽ��
����������������ϵ����д����Ӧ�ĵ�ʽ��
���𰸡���![]() ��
��![]() ����
���� ![]() ��
��![]() Ϊ
Ϊ![]() ��
��![]() ����
����![]() ��������.
��������.
�������������������1�����ݾ���ֵ����ȫƽ���ķǸ��ԣ��ɵó�a��b��ֵ���̶��ɵó��߶�AB�ij���
��2�������x��ֵ������PA+PB=PC���ɵó���P��Ӧ������
��3������A��B��C���˶����ȷ��AB��BC�ı仯������ٸ���t��ȡֵ��Χ�������AB��BC�����������ϵ��
����������⣺��1����|a��2|+��b+1��2=0����a=2��b=��1�����߶�AB�ij�Ϊ��2������1��=3��
��2���ⷽ��x��1=![]() x+1����x=3�����C�������϶�Ӧ����Ϊ3��
x+1����x=3�����C�������϶�Ӧ����Ϊ3��
![]()
��ͼ֪������PA+PB=PCʱ����P��������C���Ҳ࣬���������߶�AC�ϣ��������P�ڵ�B���ʱ��2��x+����1����x=3��x����ã�x=��2��
�۵�P��A��B֮��ʱ��3��x=3����ã�x=0��
�������P��Ӧ����Ϊ��2��0��
��3��t���Ӻ�A��λ��Ϊ��2��t��B���λ��Ϊ����1+4t��C���λ��Ϊ��3+9t��BC=3+9t������1+4t��=4+5t��AB=|��1+4t��2+t|=|5t��3|����t��![]() ʱ��AB+BC=3��5t+4+5t=7��
ʱ��AB+BC=3��5t+4+5t=7��
��t��![]() ʱ��BC��AB=4+5t����5t��3��=7��
ʱ��BC��AB=4+5t����5t��3��=7��
���Ե�t��![]() ʱ��AB+BC=7����t��
ʱ��AB+BC=7����t��![]() ʱ��BC��AB=7��
ʱ��BC��AB=7��

 �Ķ��쳵ϵ�д�
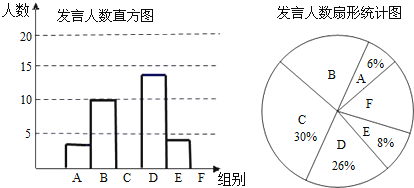
�Ķ��쳵ϵ�д�����Ŀ��ijУ2015����꼶Ϊ�˽�ѧ�����÷�������������ȡ���꼶����ѧ����������ij���ڿ����Ϸ��ԵĴ���������ͳ�ƣ��������±�������������ͼ��ʾ��������������ͳ��ͼ����֪B��E���鷢�������ı�Ϊ5��2������ͼ��������ݻش��������⣺
���Դ���n | ���� | �ٷֱ� | |
A | 0��n��3 | ||
B | 3��n��6 | ||
C | 6��n��9 | ||
D | 9��n��12 | ||
E | 12��n��15 | ||
F | 15��n��18 |
��1�������������������ȫֱ��ͼ��
��2�����꼶����ѧ��500�ˣ������ȫ�꼶��������Դ���������12�ε�������
��3����֪A�鷢�Ե�ѧ����ǡ��1λŮ����E�鷢�Ե�ѧ������2λ�������ִ�A����E���зֱ��һλѧ��д���棬�����б�������״ͼ�ķ��������������λѧ��ǡ����һ��һŮ�ĸ��ʣ�