��Ŀ����
����Ŀ���߳�Ϊ2��������OABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����D�DZ�OA���е㣬����CD����E�ڵ�һ���ޣ���DE��DC��DE=DC����ֱ��ABΪ�Գ���������߹�C��E���㣮
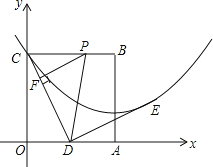
��1���������ߵĽ���ʽ��
��2����P�ӵ�C������������CBÿ��1����λ���ȵ��ٶ��˶����˶�ʱ��Ϊt�룮����P��PF��CD�ڵ�F����tΪ��ֵʱ���Ե�P��F��DΪ���������������COD���ƣ�
��3����MΪֱ��AB��һ���㣬��NΪ��������һ���㣬�Ƿ���ڵ�M��N��ʹ���Ե�M��N��D��EΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�����������ĵ�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��1��
����2��1��![]() ����3��M1��2��1����N1��4��2����M2��2��3����N2��0��2����M3��2��
����3��M1��2��1����N1��4��2����M2��2��3����N2��0��2����M3��2��![]() ����N3��2��
����N3��2��![]() ����
����
��������
�����������1�����������ε����ʣ��ɵ�OA=OC����AOC=��DGE��������ǵ����ʣ��ɵ���OCD=��GDE������ȫ�������ε��ж������ʣ��ɵ�EG=OD=1��DG=OC=2�����ݴ���ϵ�������ɵú�������ʽ��
��2���������ۣ�����DFP�ס�COD���������������ε����ʣ��ɵ���PDF=��DCO������ƽ���ߵ��ж������ʣ��ɵ���PDO=��OCP=��AOC=90�����ݾ��ε��ж������ʣ��ɵ�PC�ij�������PFD�ס�COD���������������ε����ʣ��ɵ���DPF=��DCO��![]() =
=![]() �����ݵ��������ε��ж������ʣ��ɵ�DF��CD�Ĺ�ϵ���������������ε����Ʊȣ��ɵ�PC�ij���
�����ݵ��������ε��ж������ʣ��ɵ�DF��CD�Ĺ�ϵ���������������ε����Ʊȣ��ɵ�PC�ij���
��3���������ۣ�MDNE��MNDE��NDME������һ��Ա�ƽ������ȵ��ı���ʽƽ���ıߣ��ɵô𰸣�
�����������1������E��EG��x����G�㣮���ı���OABC�DZ߳�Ϊ2�������Σ�D��OA���е㣬��OA=OC=2��OD=1����AOC=��DGE=90�����ߡ�CDE=90�㣬���ODC+��GDE=90�����ߡ�ODC+��OCD=90�㣬���OCD=��GDE������OCD����GED�����ߡ�COD=��DGE����OCD=��GDE��DC=DE�����ODC�ա�GED��AAS������EG=OD=1��DG=OC=2������E������Ϊ��3��1�����������ߵĶԳ���Ϊֱ��AB��ֱ��x=2�������������ߵĽ���ʽΪ![]() ����C��E�������������ʽ������
����C��E�������������ʽ������![]() �������
�������![]() �������ߵĽ���ʽΪ
�������ߵĽ���ʽΪ![]() ��
��
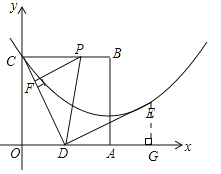
��2��������DFP�ס�COD������PDF=��DCO����PD��OC�����PDO=��OCP=��AOC=90�㣬���ı���PDOC�Ǿ��Σ���PC=OD=1����t=1��
������PFD�ס�COD������DPF=��DCO��![]() =
=![]() �����PCF=90�㩁��DCO=90����DPF=��PDF����PC=PD����DF=
�����PCF=90�㩁��DCO=90����DPF=��PDF����PC=PD����DF=![]() CD����
CD����![]() ����CD=
����CD=![]() ����DF=
����DF=![]() ����
����![]() =
=![]() ����PC=PD=
����PC=PD=![]() ��
��![]() =
=![]() ��t=
��t=![]() ��
��
����������t=1��t=![]() ʱ���Ե�P��F��DΪ���������������COD���ƣ�
ʱ���Ե�P��F��DΪ���������������COD���ƣ�
��3�����ڣ�
�ı���MDEN��ƽ���ı���ʱ��M1��2��1����N1��4��2����
�ı���MNDE��ƽ���ı���ʱ��M2��2��3����N2��0��2����
�ı���NDME��ƽ���ı���ʱ��M3��2��![]() ����N3��2��
����N3��2��![]() ����
����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ����ij�����������У����꼶һ��Ůͬѧ��һ�������������ɼ�����λ:�������±���
�� �� | 45 | 46 | 47 | 48 | 49 | 50 |
�� �� | 1 | 2 | 4 | 2 | 5 | 1 |
��˲��Գɼ�����λ���������ֱ�Ϊ�� ��
A.47, 49
B.48, 49
C.47.5, 49
D.48, 50
����Ŀ����![]() ��ʼ��������������ӣ����Ǻ͵���������ʾ��
��ʼ��������������ӣ����Ǻ͵���������ʾ��
�����ĸ��� | ���������ĺ� |
|
|
|
|
|
|
|
|
|
|
|
|
��![]() ����
����![]() ��ֵΪ__________��
��ֵΪ__________��
��![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ����������֮��
����������֮��![]() �Ĺ�ʽ��
�Ĺ�ʽ�� ![]() __________��
__________��
�ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() ��ʼ����
��ʼ����![]() ������������__________��
������������__________��
��![]() �����ݹ��ɼ���
�����ݹ��ɼ���![]() ��
��