题目内容
【题目】在平面直角坐标系中,已知:函数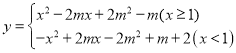 .
.
(1)当![]() 时,
时,
①求![]() 随
随![]() 增大而增大时,
增大而增大时,![]() 的取值范围;
的取值范围;
②当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
③当![]() 时,设
时,设![]() 的最大值与最小值之差为
的最大值与最小值之差为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
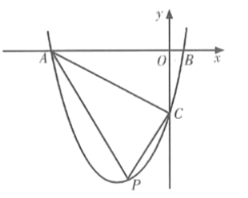
(2)若![]() ,连结
,连结![]() .当此函数的图象与线段
.当此函数的图象与线段![]() 只有两个公共点时,直接写出
只有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①![]() 或
或![]() ;②
;②![]() ;③
;③![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)①利用函数图像,直接作答即可;
②观察函数图像直接作答即可;
③分![]() 、
、![]() 、
、![]() 、
、![]() 四种情况分类讨论即可;
四种情况分类讨论即可;
(2)利用两个函数的对称轴都是直线![]() ,分类讨论
,分类讨论![]() 所处的位置,即可得出答案.
所处的位置,即可得出答案.
(1)①![]() 或
或![]() .
.
当![]() 时,函数变为
时,函数变为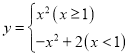 ,
,
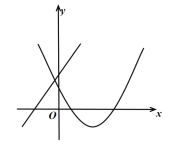
函数图像如图所示:
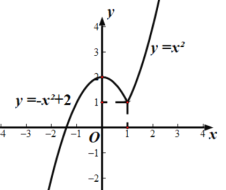
函数![]() 的对称轴是直线
的对称轴是直线![]() ,
,
所以通过观察图像可以得到当![]() 随
随![]() 增大而增大时,
增大而增大时,![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ;
;
②![]() ;
;
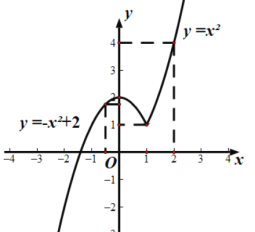
通过观察图像可以得到:当![]() 时,
时,![]() ;
;
③当![]() ,即
,即![]() 时,
时,
![]()
![]() ,
,![]()
当![]() 时,由图象可知
时,由图象可知![]()
当![]() 时,
时,![]()
由![]() ,
,
得![]() ,
,
![]()
![]()
当![]() 时,
时,![]()
![]()
![]()
![]() 舍去.
舍去.
综上所述:![]() 或
或![]() ;
;

![]() 或
或![]() 或
或![]() ,
,
∵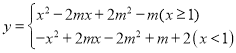
∴![]() 的对称轴为直线:
的对称轴为直线:![]() ,
,
![]() 的对称轴为直线:
的对称轴为直线:![]() ,
,
①由(1)可知:当![]() 时,函数与AB有两个交点,一个为(0,2),一个为(
时,函数与AB有两个交点,一个为(0,2),一个为(![]() ),满足条件;
),满足条件;
②当![]() 时,函数变为:
时,函数变为: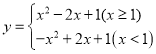 ,此时只有一个交点
,此时只有一个交点![]() ,不合题意;
,不合题意;
③当![]() 时,函数变为:
时,函数变为: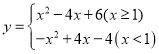 ,此时只有一个交点
,此时只有一个交点![]() ,不合题意;
,不合题意;
④当![]() 时,此时
时,此时![]() 的顶点坐标为
的顶点坐标为![]() ,
,
∵![]() ,
,
∴![]() 与AB无交点;
与AB无交点;
对于函数![]() 一直小于0,因此与AB无交点;
一直小于0,因此与AB无交点;
⑤当![]() 时,
时,
对于函数![]() 来说,当
来说,当![]() 时,有最小值此时
时,有最小值此时![]() ,因此函数
,因此函数![]() 与AB最多有一个交点,
与AB最多有一个交点,
对于函数![]() ,当
,当![]() 时,有最大值,为
时,有最大值,为![]() ,与AB无交点;
,与AB无交点;
⑥当![]() 时,
时,
对于函数![]() 来说,
来说,![]() ,因此与AB必有一个交点,
,因此与AB必有一个交点,
只须保证:![]() 与AB有一个交点即可,
与AB有一个交点即可,
当![]() 时,当
时,当![]() 时,有最大值为
时,有最大值为![]() ,根据对称性可知:此时与AB有两个交点,
,根据对称性可知:此时与AB有两个交点,
∴当![]() 时,有三个交点,不合题意;
时,有三个交点,不合题意;
当![]() 时,
时,
函数变为: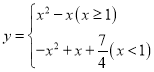 ,此时与AB共有两个交点;
,此时与AB共有两个交点;
当![]() 时:
时:![]() 与AB有一个交点,
与AB有一个交点,
∴此时函数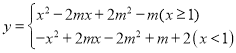 与AB有两个交点;
与AB有两个交点;
⑦当![]() 时,
时,
对于函数![]() :
:![]() ,与AB无交点,
,与AB无交点,
当函数![]() 过
过![]() 时,
时,
得:![]() ,解得:
,解得:![]() ,
,
∵![]() ,
,
∴![]() ,此时与AB有两个交点,
,此时与AB有两个交点,
∴当![]() 时,
时,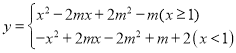 与AB有两个交点;
与AB有两个交点;
综上所述:当![]() 或
或![]() 或
或![]() 时,
时,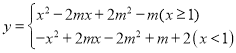 与AB只有两个交点.
与AB只有两个交点.