题目内容
【题目】如图,在每个边长都为![]() 的小正方形组成的网格中,小正方形的顶点叫做格点.线段
的小正方形组成的网格中,小正方形的顶点叫做格点.线段![]() 的端点
的端点![]() 均在格点上.
均在格点上.
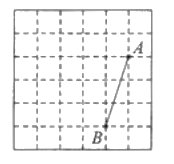
(1)线段![]() 的长度等于 ;
的长度等于 ;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,在图中画出
,在图中画出![]() ,并连结
,并连结![]() .
.
(3)在线段![]() 上确定一点
上确定一点![]() 连结
连结![]() ,使得
,使得![]() 与
与![]() 的面积比为
的面积比为![]() .
.
说明:以上作图只用无刻度的直尺画图,保留画图痕迹,不写画法.
【答案】(1)![]() ;(2)如图所示见解析;(3)如图所示见解析.
;(2)如图所示见解析;(3)如图所示见解析.
【解析】
(1)结合格点图形,利用勾股定理求解即可;
(2)依据旋转方式作图即可,注意线段BC的长与AB的长相等;
(3)利用平行线构造相似三角形,使对应边AD与BD的比为3:4,从而得到等高的两三角形![]() 与
与![]() 的面积比为
的面积比为![]() .
.
解:(1)结合图形,由勾股定理得:![]()
(2)如图所作,
(3)如图所示,在格点上取点M、N,使得BM=4,AN=3,连接MN,交AB于点D,连接CD则![]() 与
与![]() 的面积比为
的面积比为![]() ,理由如下:
,理由如下:
因为BM//AN,易知![]() ∽
∽![]() ,∴
,∴![]() ,过点C作CH⊥AB,则
,过点C作CH⊥AB,则

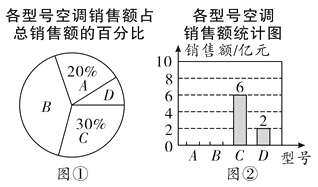
【题目】某体育器材专卖柜经销A、B两种器材,A种器材每件进价350元,售价480元;B种器材每件进价200元,售价300元.
(1)该专卖柜计划用8000元去购进A、B两种器材若干件.
①若购进A种器材x件,B种器材y件,所获利润w元,请写出w与x之间满足的函数关系式;
②怎样购进才能使专卖柜经销这两种器材所获利润最大(其中A种器材不少于7件)?
(2)在“五·一”期间,该专卖柜对A、B两种器材进行如下优惠促销活动:
一次性购物总金额 | 优惠措施 |
不超过3000元 | 不优惠 |
超过3000元不超过4000元 | 售价打八折 |
超过4000元 | 售价打七折 |
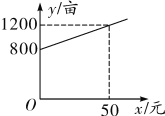
促销活动期间:甲学校去该专卖柜购买A种器材付款2688元;乙学校去该专卖柜购买B种器材付款2100元,求丙学校决定一次性购买甲学校和乙学校购买的同样多的器材需付款多少元?
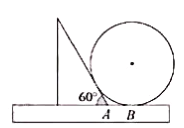
【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)