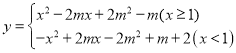题目内容
【题目】在平面直角坐标系xOy中,已知点A,对点A作如下变换:
第一步:作点A关于x轴的对称点A1;第二步:以O为位似中心,作线段OA1的位似图形OA2,且相似比![]() =q,则称A2是点A的对称位似点.
=q,则称A2是点A的对称位似点.
(1)若A(2,3),q=2,直接写出点A的对称位似点的坐标;
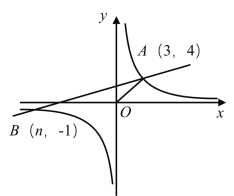
(2)已知直线l:y=kx-2,抛物线C:y=-![]() x2+mx-2(m>0).点N(
x2+mx-2(m>0).点N(![]() ,2k-2)在直线l上.
,2k-2)在直线l上.
①当k=![]() 时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
②若直线l与抛物线C交于点M(x1,y1)(x1≠0),且点M不是抛物线的顶点,则点M的对称位似点是否可能仍在抛物线C上?请说明理由.
【答案】(1)![]() 、
、![]() ;(2)①E(1,-1)不是N(2,-1)的对称位似点;②
;(2)①E(1,-1)不是N(2,-1)的对称位似点;②![]() .理由见解析.
.理由见解析.
【解析】
(1)由对称位似点的定义可求出点A的对称位似点的坐标;
(2)①先求出N点坐标为(2,1),关于x轴的对称点坐标为(2,1),由E(1,1),
![]() ,故不存在q,使得E(1,1)是点N的对称位似点,可知E(1,1)不是点N的对称位似点;
,故不存在q,使得E(1,1)是点N的对称位似点,可知E(1,1)不是点N的对称位似点;
②把N点坐标代入y=kx2,可得m=2k或m=k,当直线与二次函数图象相交时求得M(4k,4k22),![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,求出直线
,求出直线![]() 的解析式,联立方程组,当△≥0时,求得
的解析式,联立方程组,当△≥0时,求得![]() 时,点M的对称位似点仍在抛物线C上.
时,点M的对称位似点仍在抛物线C上.
解:(1)∵A(2,3),
∴A关于x轴的对称点A1为(2,3)),
∵以O为位似中心,作线段OA1的位似图形OA2,且相似比为2,
∴A2的坐标为(4,6)或(-4,6),
∴A的对称位似点的坐标为(4,6)或(4,6).
![]() 、
、![]()
(2)①当![]() 时,
时,![]() ,将
,将![]() 代入
代入![]() 得:
得:![]()
![]()
![]() 的坐标为
的坐标为![]() ,其关于
,其关于![]() 轴的对称点坐标是
轴的对称点坐标是![]()
对于![]() ,
,
![]() ,所构成的
,所构成的![]() 直角边不成比例,
直角边不成比例,
![]() 不是
不是![]() 的对称位似点
的对称位似点
②直线![]() :
:![]() 过点
过点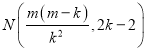
![]() ,整理得:
,整理得:![]()
![]()
![]() 或
或![]()
直线与抛物线相交于点![]() :
:![]()
![]()
![]() ,
,![]() ,
,![]()
抛物线对称轴:![]() ,且点
,且点![]() 不是抛物线的顶点
不是抛物线的顶点
![]() ,
,![]()
![]() 只有
只有![]() 成立. 此时,
成立. 此时,![]()
![]() 的坐标:
的坐标:![]()
于是,![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,
直线![]() 的解析式:
的解析式:![]()
若直线![]() 与抛物线有相交,
与抛物线有相交,![]()
整理得:![]()
当![]() ,
,![]() 时,交点存在,不妨设为
时,交点存在,不妨设为![]() ,
,![]() ,
,
则![]() 是点
是点![]() 的对称位似点
的对称位似点
![]() ,且
,且![]() ,
,
![]() ,
,
![]() .
.

【题目】在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【题目】某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量y(台)与销售单价x(元)的关系可以近似地看做一次函数,如下表所示:
x | 22 | 24 | 26 | 28 |
y | 90 | 80 | 70 | 60 |
(1)请直接写出y与x之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为ω(元),求ω与x之间的函数关系式,当x取何值时,ω的值最大?最大值是多少?