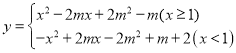题目内容
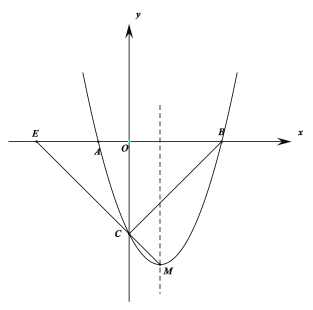
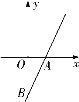
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,且
,且![]() ,点
,点![]() 是第三象限内抛物线上的一动点.
是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)(
;(2)(![]() ,
,![]() );(3)
);(3)![]() 面积的最大值是8;点
面积的最大值是8;点![]() 的坐标为(
的坐标为(![]() ,
,![]() ).
).
【解析】
(1)由二次函数的性质,求出点C的坐标,然后得到点A、点B的坐标,再求出解析式即可;
(2)由![]() ,则点P的纵坐标为
,则点P的纵坐标为![]() ,代入解析式,即可求出点P的坐标;
,代入解析式,即可求出点P的坐标;
(3)先求出直线AC的解析式,过点P作PD∥y轴,交AC于点D,则![]() ,设点P为(
,设点P为(![]() ,
,![]() ),则点D为(
),则点D为(![]() ,
,![]() ),求出PD的长度,利用二次函数的性质,即可得到面积的最大值,再求出点P的坐标即可.
),求出PD的长度,利用二次函数的性质,即可得到面积的最大值,再求出点P的坐标即可.
解:(1)在抛物线![]() 中,
中,
令![]() ,则
,则![]() ,
,
∴点C的坐标为(0,![]() ),
),
∴OC=2,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴点A为(![]() ,0),点B为(
,0),点B为(![]() ,0),
,0),
则把点A、B代入解析式,得
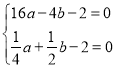 ,解得:
,解得:![]() ,
,
∴![]() ;
;
(2)由题意,∵![]() ,点C为(0,
,点C为(0,![]() ),
),
∴点P的纵坐标为![]() ,
,
令![]() ,则
,则![]() ,
,
解得:![]() ,
,![]() ,
,
∴点P的坐标为(![]() ,
,![]() );
);
(3)设直线AC的解析式为![]() ,则
,则
把点A、C代入,得
![]() ,解得:
,解得: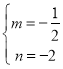 ,
,
∴直线AC的解析式为![]() ;
;
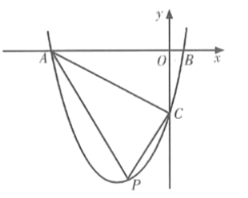
过点P作PD∥y轴,交AC于点D,如图:
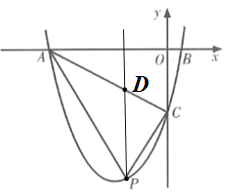
设点P 为(![]() ,
,![]() ),则点D为(
),则点D为(![]() ,
,![]() ),
),
∴![]() ,
,
∵OA=4,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 取最大值8;
取最大值8;
∴![]() ,
,
∴点P的坐标为(![]() ,
,![]() ).
).

【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)