题目内容
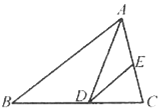
【题目】已知⊙O的半径为5,EF是长为8的弦,OG⊥EF于点G,点A在GO的延长线上,且AO=13.弦EF从图1的位置开始绕点O逆时针旋转,在旋转过程中始终保持OG⊥EF,如图2.
[发现]在旋转过程中,
(1)AG的最小值是 ,最大值是 .
(2)当EF∥AO时,旋转角α= .
[探究]若EF绕点O逆时针旋转120°,如图3,求AG的长.
[拓展]如图4,当AE切⊙O于点E,AG交EO于点C,GH⊥AE于H.
(1)求AE的长.
(2)此时EH= ,EC= .

【答案】发现:(1)10,16;(2)90°或270°;探究:AG=![]() ;拓展:(1)AE=12;(2)
;拓展:(1)AE=12;(2)![]() ,
,![]() .
.
【解析】
发现:(1)根据垂径定理得:![]() 在Rt△EOG中,根据勾股定理求出OG=3,由旋转知,点G的轨迹是以点O为圆心,OG=3为半径的圆,即可求出AG的最大值与最小值.
在Rt△EOG中,根据勾股定理求出OG=3,由旋转知,点G的轨迹是以点O为圆心,OG=3为半径的圆,即可求出AG的最大值与最小值.
(2)根据OG⊥EF,EF∥OA,得出OG⊥OA,即可求出旋转角度.
探究:过点G作GQ⊥OA于Q,在Rt△OQG中,求出∠GOQ的度数,根据含![]() 角的直角三角形的性质求出
角的直角三角形的性质求出![]() 即可求出AG的长
即可求出AG的长
拓展:(1)根据切线的性质得到∠OEA=90°,根据勾股定理即可求出AE的长.
(2)过点G作GP⊥OE于P,易证四边形EHGP是矩形,证明△OGE∽△OPG,根据相似三角形的性质得到![]() 即可求出
即可求出![]() 的长度,即可求出EH的长度,再根据△AEC∽△AHG,求出EC的长度.
的长度,即可求出EH的长度,再根据△AEC∽△AHG,求出EC的长度.
发现:(1)如图1,
连接OE,
∵OG⊥EF,
∴![]()
在Rt△EOG中,OE=5,根据勾股定理得,OG=3,
由旋转知,点G的轨迹是以点O为圆心,OG=3为半径的圆,
∴AG最大=OA+OG=13+3=16,
AG最小=OA﹣OG=13﹣3=10,
故答案为:10,16;
(2)∵OG⊥EF,EF∥OA,
∴OG⊥OA,
∴旋转角α=90°或270°,
故答案为90°或270°;
探究:如图3,
过点G作GQ⊥OA于Q,
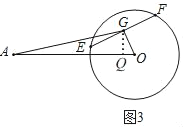
在Rt△OQG中,∠GOQ=180°﹣120°=60°,OG=3,
∴![]()
∴![]()
在Rt△AQG中, ![]()
拓展:(1)∵AE切⊙O于E,
∴∠OEA=90°,
在Rt△AEO中,![]()
(2)如图4,
过点G作GP⊥OE于P,
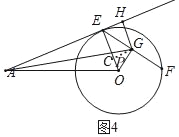
∵HG⊥AE,OE⊥AE,
∴四边形EHGP是矩形,
∴HG=EP,EH=PG,
∵∠OGE=∠OPG=90°,∠GOE=∠POG,
∴△OGE∽△OPG,
∴![]()
∴![]()
∴![]()
∴![]()
![]()
∵OE⊥AE,HG⊥AE,
∴CE∥HG,
∴△AEC∽△AHG,
∴![]()
∴![]()
∴![]()
故答案为:![]()