题目内容
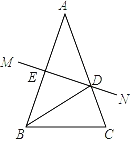
【题目】已知:在等边△ABC中, AB=![]() , D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
, D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
(1)判断△BDE的形状;

(2)在图2中补全图形,
①猜想在旋转过程中,线段CE1与AD1的数量关系并证明;
②求∠APC的度数;
(3)点P到BC所在直线的距离的最大值为________.(直接填写结果)

 、
、
图2 备用
【答案】(1)等边三角形;
(2)①见解析;②见解析.
【解析】
(1)由D、E分别是AB、BC的中点得到![]() ,
,![]() ,加上
,加上![]() 为等边三角形,则
为等边三角形,则![]() ,
,![]() ,所以
,所以![]() ,于是可判断
,于是可判断![]() 为等边三角形;
为等边三角形;
(2)①根据旋转的性质得![]() 为等边三角形,则
为等边三角形,则![]() ,
,![]() ,而
,而![]() ,所以∠D1BA=∠E1BC,则可证明△ABD1≌△CBE1,所以CE1=AD1;
,所以∠D1BA=∠E1BC,则可证明△ABD1≌△CBE1,所以CE1=AD1;
②由△ABD1≌△CBE1,可得到∠D1AB=∠E1CB,即可得到∠APC=∠ABC;
(3)由于![]() ,则可判断点P、D1、B、E1共圆,于是可判断当
,则可判断点P、D1、B、E1共圆,于是可判断当![]() 时,点P到BC所在直线的距离的最大值,此时点E在AB上,然后利用含30度的直角三角形三边的关系可得点P到BC所在直线的距离的最大值.
时,点P到BC所在直线的距离的最大值,此时点E在AB上,然后利用含30度的直角三角形三边的关系可得点P到BC所在直线的距离的最大值.
解:
(1)等边三角形.
(2)补全图形如右图.
①CE1=AD1.
∵ △ABC和△BD1E1为等边三角形,
∴ BC=BA,BE1=BD1,∠ABC=∠D1BE1=60°.
∴ ∠ABC-∠ABE1 =∠D1BE1-∠ABE1.
即∠D1BA=∠E1BC.
∴ △ABD1≌△CBE1.
∴ CE1=AD1.
②∵ △ABD1≌△CBE1,
∴ ∠D1AB=∠E1CB.
又∵∠D1AB+∠APC=∠ABC+∠E1CB,
∴ ∠APC=∠ABC=60°.
(3)2.

练习册系列答案
相关题目