题目内容
【题目】已知点M（n，﹣n ）在第二象限，过点M的直线y=kx+b（0＜k＜1）分别交x轴、y轴于点A，B，过点M作MN⊥x轴于点N，则下列点在线段AN的是（ ）
A. （（k﹣1）n，0） B. （（k+
）n，0）） C. （
，0） D. （（k+1）n，0）
【答案】D
【解析】
如图所示，过M作MC⊥y轴于C，
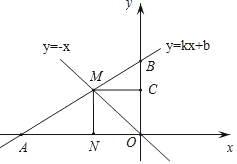
∵M（n，﹣n ），MN⊥x轴于点N，
∴C（0，﹣n），N（n，0），
把M（n，﹣n ）代入直线y=kx+b，可得b=﹣n﹣kn，
∴y=kx﹣n（1+k），
令x=0，则y=﹣n（1+k），即B（0，﹣n（1+k），
∴﹣n（1+k）＞﹣n，
∴n（1+k）＜n，
令y=0，则0=kx﹣n（1+k），
解得x=
=n（
+1），即A[n（+1），0）]，
∵0＜k＜1，n＜0，
∴n（+1）＜n（1+k）＜n，
∴点[（k+1）n，0]在线段AN上．
故选：D．
练习册系列答案
阅读快车系列答案
相关题目
