Question

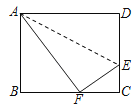
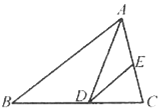
【题目】如图，在△ABC中，2BD=3DC，E是AC的中点，如S△ABC=10，则S△ADE=( )

A.5B.4 C.3 D.2

Answer 1

【答案】D

【解析】

由已知可证得BD：DC=3:2，由此可推出S△ABD：S△ADC=3：2，再根据S△ABD+S△ADC= S△ABC=10 ，求出△ADC的面积，然后根据三角形的中线分得的两个三角形的面积相等，可求出△ADE的面积.

解：∵2BD=3DC，

∴BD：DC=3：2，

∴S△ABD：S△ADC=3：2，

设S△ABD=3x，S△ADC=2x，

∵S△ABD+S△ADC= S△ABC=10，

∴3x+2x=10，

解得：x=2，

∴S△ADC=2×2=4，

∵点E是AC的中点，即DE是△ADC的中线，

∴S△ADC=2S△ADE=4，

∴S△ADE=2，

故答案为：D.