��Ŀ����
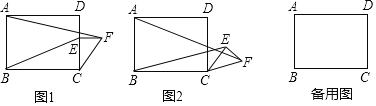
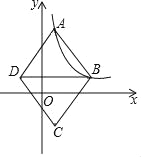
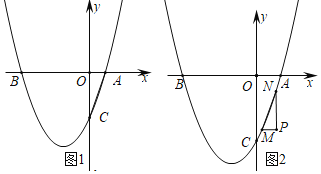
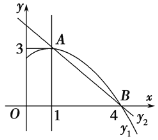
����Ŀ����ͼ��������y1��ax2��bx��c(a��0)ͼ���һ���֣������ߵĶ�������A(1��3)����x���һ������B(4��0)��ֱ��y2��mx��n(m��0)�������߽���A��B���㣬���н��ۣ���2a��b��0����abc>0���۷���ax2��bx��c��3��������ȵ�ʵ����������������x�����һ��������(��1��0)������1<x<4ʱ����y2<y1��������ȷ���ǣ���
A.�٢ܢ�B.�٢ۢܢ�C.�٢ۢ�D.�٢ڢ�
���𰸡�C
��������
�ٸ��ݶԳ���x=1��ȷ��a��b�Ĺ�ϵ��Ȼ���ж����ɣ�
�ڸ���ͼ��ȷ��a��b��c�ķ��ţ������ж���
�۷���ax2+bx+c=3�ĸ�����y=3��ͼ���������߽���ĺ������ж����ɣ�
�ܸ��ݶԳ����жϼ��ɣ�
����ͼ��ɵã���1<x<4ʱ������������ֱ�ߵ����棬��y2<y1��
�⣺�١߶Գ���Ϊ��x=1��
��![]() ��a=-2b,��2a+b=0���ʢ���ȷ;
��a=-2b,��2a+b=0���ʢ���ȷ;
�������߿�������
��a��0
���Գ�����y���Ҳ࣬
��b��0
����������y�ύ��������
��c��0
��abc<0,�ʢڲ���ȷ��
�������ߵĶ�������A��1,3��
���ax2+bx+c=3��������ȵ�ʵ������x=1���ʢ���ȷ��
�������߶Գ����ǣ�x=1��B��4,0����
����������x�����һ�������ǣ�-2,0���ʢܴ���
��ͼ��ã���1<x<4ʱ����y2<y1���ʢ���ȷ��
�ʴ�ΪC��

����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�