题目内容
【题目】问题探究
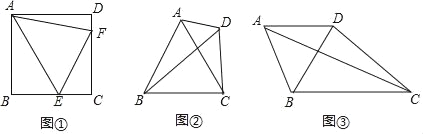
(1)如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,则线段BE、EF、FD之间的数量关系为 ;
(2)如图②,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边△ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;
问题解决
(3)如图③,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
【答案】(1)BE+DF=EF;(2)存在,BD的最大值为6;(3)存在,AC的最大值为2![]() +2
+2![]() .
.
【解析】
(1)作辅助线,首先证明△ABE≌△ADG,再证明△AEF≌△AEG,进而得到EF=FG问题即可解决;
(2)将△ABD绕着点B顺时针旋转60°,得到△BCE,连接DE,由旋转可得,CE=AD=2,BD=BE,∠DBE=60°,可得DE=BD,根据DE<DC+CE,则当D、C、E三点共线时,DE存在最大值,问题即可解决;
(3)以BC为边作等边三角形BCE,过点E作EF⊥BC于点F,连接DE,由旋转的性质得△DBE是等边三角形,则DE=AC,根据在等边三角形BCE中,EF⊥BC,可求出BF,EF,以BC为直径作⊙F,则点D在⊙F上,连接DF,可求出DF,则AC=DE≤DF+EF,代入数值即可解决问题.
(1)如图①,延长CD至G,使得DG=BE,
∵正方形ABCD中,AB=AD,∠B=∠AFG=90°,
∴△ABE≌△ADG,
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=45°,∠BAD=90°,
∴∠BAE+∠DAF=45°,
∴∠DAG+∠DAF=45°,即∠GAF=∠EAF,
又∵AF=AF,
∴△AEF≌△AEG,
∴EF=GF=DG+DF=BE+DF,
故答案为:BE+DF=EF;
(2)存在.
在等边三角形ABC中,AB=BC,∠ABC=60°,
如图②,将△ABD绕着点B顺时针旋转60°,得到△BCE,连接DE.
由旋转可得,CE=AD=2,BD=BE,∠DBE=60°,
∴△DBE是等边三角形,
∴DE=BD,
∴在△DCE中,DE<DC+CE=4+2=6,
∴当D、C、E三点共线时,DE存在最大值,且最大值为6,
∴BD的最大值为6;
(3)存在.
如图③,以BC为边作等边三角形BCE,过点E作EF⊥BC于点F,连接DE,
∵AB=BD,∠ABC=∠DBE,BC=BE,
∴△ABC≌△DBE,
∴DE=AC,
∵在等边三角形BCE中,EF⊥BC,
∴BF=![]() BC=2
BC=2![]() ,
,
∴EF=![]() BF=
BF=![]() ×2
×2![]() =2
=2![]() ,
,
以BC为直径作⊙F,则点D在⊙F上,连接DF,
∴DF=![]() BC=
BC=![]() ×4
×4![]() =2
=2![]() ,
,
∴AC=DE≤DF+EF=2![]() +2
+2![]() ,即AC的最大值为2
,即AC的最大值为2![]() +2
+2![]() .
.

 阅读快车系列答案
阅读快车系列答案