题目内容
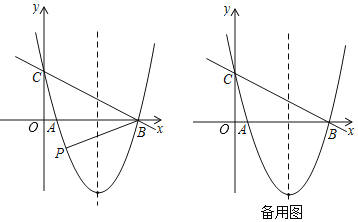
【题目】在平面直角坐标系中,已知二次函数y=ax2﹣2ax﹣3a(a>0)图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)求点A,B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM.
①求二次函数解析式;
②当t﹣2≤x≤t时,二次函数有最大值5,求t值;
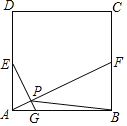
③若直线x=4与此抛物线交于点E,将抛物线在C,E之间的部分记为图象记为图象P(含C,E两点),将图象P沿直线x=4翻折,得到图象Q,又过点(10,﹣4)的直线y=kx+b与图象P,图象Q都相交,且只有两个交点,求b的取值范围.
【答案】(1)A(﹣1,0)、B(3,0);(2)①y=x2﹣2x﹣3;②t值为0或4;③﹣1≤b<11或b=﹣4.
【解析】
(1)令y=0,即:ax2﹣2ax﹣3a=0,解得:x=﹣1或3,即可求解;
(2)①DM=2AM=4,即点D的坐标为(1,﹣4),将点D的坐标代入二次函数表达式,即可求解;
②分x=t和x=t﹣2在对称轴右侧、左侧或两侧三种情况,讨论求解即可;
③如下图所示,直线m、l、n都是直线y=kx+b与图象P、Q都相交,且只有两个交点的临界点,即可求解.
解:(1)令y=0,即:ax2﹣2ax﹣3a=0,解得:x=﹣1或3,
即点A、B的坐标分别为(﹣1,0)、(3,0),函数的对称轴![]()
(2)①DM=2AM=4,即点D的坐标为(1,﹣4),
将点D的坐标代入二次函数表达式得:
﹣4=a﹣2a﹣3a,解得:a=1,即函数的表达式为:y=x2﹣2x﹣3;
②当x=t和x=t﹣2在对称轴右侧时,函数在x=t处,取得最大值,
即:t2﹣2t﹣3=5,解得:t=﹣2或4(舍去t=﹣2),即t=4;
同理当x=t和x=t﹣2在对称轴左侧或两侧时,解得:t=0,
故:t值为0或4;
③如下图所示,直线m、l、n都是直线y=kx+b与图象P、Q都相交,且只有两个交点的临界点,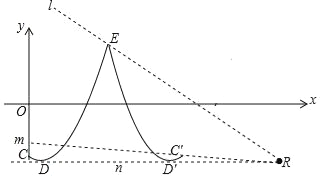
点E、R、C'坐标分别为(4,5)、(10,﹣4)、(8,﹣3),直线l的表达式:把点E、R的坐标代入直线y=kx+b得:
![]() 解得:
解得: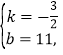
同理可得直线m的表达式为:![]()
直线n的表达式为:y=﹣4,故:b的取值范围为:﹣1≤b<11或b=﹣4.

 名校课堂系列答案
名校课堂系列答案