题目内容
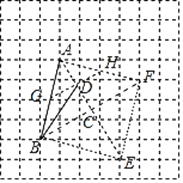
【题目】在每个小正方形的边长为1的网格中,点A、B均为格点.

(Ⅰ)AB的长等于_____.
(Ⅱ)若点C是以AB为底边的等腰直角三角形的顶点,点D在边AC上,且满足S△ABD=![]() S△ABC.请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置是如何找到的(不要求证明)______.
S△ABC.请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置是如何找到的(不要求证明)______.
【答案】![]() 以
以![]() 为边连接格点,构成正方形
为边连接格点,构成正方形![]() ,连接对角线
,连接对角线![]() 、
、![]() ,则对角线交点即为
,则对角线交点即为![]() 点,正方形相邻两边分别与网格线有两个交点
点,正方形相邻两边分别与网格线有两个交点![]() 、
、![]() ,且为两边中点,连接
,且为两边中点,连接![]() 与
与![]() 交于
交于![]() 点,连接
点,连接![]() ,
,![]() 即为所求.
即为所求.
【解析】
(Ⅰ)利用勾股定理求出AB的长即可;(Ⅱ)根据正方形的性质可得点C的位置,根据
如图,以AB为边连接格点,构成正方形ABEF,连接对角线AE、BF,
∴对角线交点即为C点,
∵正方形相邻两边分别与网格线有两个交点G、H,且为两边中点,连接GH与AE交于D点,连接BD,
∴点D为AC中点,
∴S△ABD=![]() S△ABC.
S△ABC.
∴BD即为所求.

练习册系列答案
相关题目
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?