题目内容
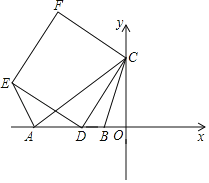
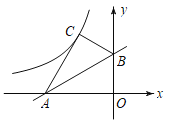
【题目】如图,已知直线![]() 与x轴,y轴分别交于点A,B,将△ABO沿直线AB翻折后得到△ABC,若反比例函数
与x轴,y轴分别交于点A,B,将△ABO沿直线AB翻折后得到△ABC,若反比例函数![]() (x<0)的图象经过点C,则k=______.
(x<0)的图象经过点C,则k=______.
【答案】![]()
【解析】
先由直线解析式求出A、B两点坐标,进而得到∠A、∠B的度数,连接OC交AB于D,求出OD的长,由轴对称性可得OC 的长,过C作CE⊥x轴于点E,通过解直角三角形求出OE、CE的长即可. ![]()
对于![]() ,当x=0时,y=2;当y=0时,x=-2
,当x=0时,y=2;当y=0时,x=-2![]() ,
,
∴A(-2![]() ,0),B(0,2)
,0),B(0,2)
∴AO=2![]() ,OB=2,
,OB=2,
∴tan∠OAB=![]() ,
,
∴∠OAB=30°
∴∠OBA=60°,
连接OC,过点C作CE⊥x轴,垂足为E,
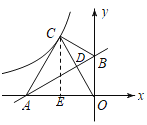
由翻折得,OD⊥AB,OD=CD,
∴OD=![]() OA=
OA=![]() ,∠AOD=60°,
,∠AOD=60°,
∴OC=2![]() ,∠OCE=30°
,∠OCE=30°
∴OE=![]() OC=
OC=![]() ,
,
∴CE=![]()
∴C(-![]() ,3)
,3)
∴k=![]() .
.
故答案为:![]() .
.

【题目】为推动实施健康中国战略,树立国家健康形象.手机APP推出多款健康运动软件,如“微信运动”.王老师随机调查了我校50名教师某日“微信运动”中的步数,并进行统计整理,绘制了如下的统计图表.
步数 | 频数 | 频率 |
| 8 |
|
| 15 | 0.3 |
|
| 0.24 |
| 10 | 0.2 |
| 3 | 0.06 |
| 2 | 0.04 |
合计 | 50 |
|
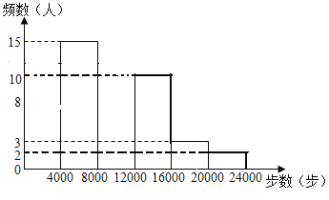
请根据以上信息,解答下列问题:
(1)![]() _______,
_______,![]() _______,
_______,![]() ________;
________;
(2)补全频数分布直方图;
(3)若某人一天的走路步数不低于16000步,将被“微信运动”评为“运动达人”.我市市区约有4000名初中教师,根据此项调查请估计市区被评为“运动达人”教师有多少名?
【题目】某超市以20元/kg的价格购进一批商品进行销售,根据以往的销售经验及对市场行情的调研,该超市得到日销售量y(kg)与销售价格x(元/kg)之间的关系,部分数据如下表:
销售价格x(元/kg) | 25 | 30 | 35 | 40 | … |
日销售量y(kg) | 1000 | 800 | 600 | 400 | … |
(1)根据表中的数据,用所学过的函数知识确定y与x之间的函数关系式;
(2)超市应如何确定销售价格,才能使日销售利润W(元)最大?W最大值为多少?
(3)供货商为了促销,决定给予超市a元/kg的补贴,但希望超市在30≤x≤35时,最大利润不超过10240元,求a的最大值.