题目内容
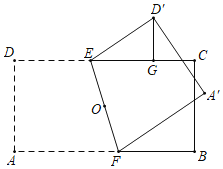
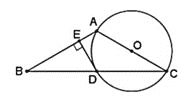
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,求线段DP的长.
,求线段DP的长.
【答案】(1)见解析;(2)见解析;(3)15
【解析】
(1)先判断出∠BAC=2∠BAD,进而判断出∠BOD=∠BAC=90°,得出PD⊥OD即可得出结论;
(2)先判断出∠ADB=∠P,再判断出∠DCP=∠ABD,即可证明△ABD∽△DCP,进一步可得出结论;
(3)首先求出BC=10,从而得出OD=5,作CG⊥DP,则可得四边形ODGC是正方形,故可得CG=5,由![]() 可求出GP=
可求出GP=![]() ,从而可得结论.
,从而可得结论.
(1)如图,连接OD,

∵BC是⊙O的直径,
∴∠BAC=90°,
∵AD平分∠BAC,
∴∠BAC=2∠BAD,
∵∠BOD=2∠BAD,
∴∠BOD=∠BAC=90°,
∵DP∥BC,
∴∠ODP=∠BOD=90°,
∴PD⊥OD,
∵OD是⊙O半径,
∴PD是⊙O的切线;
(2)∵PD∥BC,
∴∠ACB=∠P,
∵∠ACB=∠ADB,
∴∠ADB=∠P,
∵∠ABD+∠ACD=180°,∠ACD+∠DCP=180°,
∴∠DCP=∠ABD,
∴△ABD∽△DCP,
∴![]()
∴ABCP=BDCD.
(3)在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则四边形
,则四边形![]() 为正方形,
为正方形,

∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,即
,即![]() ,
,
解得,![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目