Question

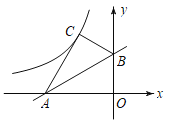
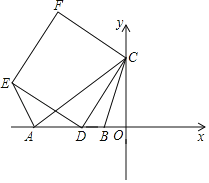
【题目】如图，在平面直角坐标系中，点A、B在x轴上，点C在y轴上，AB＝BC＝5，AC＝8，D为线段AB上一动点，以CD为边在x轴上方作正方形CDEF，连接AE．

（1）若点B的坐标为(m，0)，则m＝　 　；

（2）当BD＝　 　时，EA⊥x轴；

（3）当点D由点B运动到点A过程中，点F经过的路径长为　 　；

（4）当△ADE面积最大时，求出BD的长及△ADE面积最大值．

Answer 1

【答案】（1）﹣；（2）；（3）5；（4）BD＝，△ADE面积最大值为

【解析】

（1）由勾股定理可得64﹣（5﹣m）2＝25﹣（﹣m）2，可求m的值；

（2）由勾股定理可求CO的长，由“AAS”可证△AED≌△ODC，可得AD＝CO，即可求解；

（3）由“AAS”可证△CFH≌△CDO，可得CH＝CO＝，FH＝DO，可得点F在FH上移动，由特殊位置可求解；

（4）过点E作EN⊥x轴于点N，由三角形的面积公式可得△ADE面积＝×AD×EN＝（5﹣BD）（+BD）＝﹣（BD﹣）2+，由二次函数的性质可求解．

解：（1）∵点B的坐标为（m，0），

∴BO＝﹣m，

∵CO2＝AC2﹣AO2，CO2＝CB2﹣BO2，

∴64﹣（5﹣m）2＝25﹣（﹣m）2，

∴m＝﹣，

故答案为：﹣；

（2）∵点B的坐标为（﹣，0），

∴BO＝，

∴CO＝＝，

∵EA⊥x轴，

∴∠EAD＝90°，

∴∠EDA+∠AED＝90°，

∵四边形CDEF是正方形，

∴CD＝DE，∠EDC＝90°，

∴∠EDA+∠CDO＝90°，

∴∠AED＝∠CDO，

∵∠EAD＝∠COD，ED＝CD，

∴△AED≌△ODC（AAS）

∴AE＝DO，AD＝CO＝，

∴BD＝AB﹣AD＝5﹣＝，

∴当BD＝时，EA⊥x轴；

故答案为：；

（3）如图，过点C作CH⊥y轴，过点F作FH⊥CH，交点为H，

∵四边形CDEF是正方形，

∴CD＝CF，∠FCD＝90°，

∴∠FCH+∠DCH＝90°，

又∵∠DCO+∠HCD＝90°，

∴∠FCH＝∠DCO，

又∵FC＝DC，∠CHF＝∠DOC＝90°，

∴△CFH≌△CDO（AAS）

∴CH＝CO＝，FH＝DO，

∴点F在FH上移动，

当点D与点B重合时，FH＝BO＝，

当点D与点BC重合时，FH＝AO＝AB+BO＝5+＝，

∴当点D由点B运动到点A过程中，点F经过的路径长为﹣＝5，

故答案为：5；

（4）如图，过点E作EN⊥x轴于点N，

由（2）可得△DEN≌△CDO，

∴EN＝DO，

∵△ADE面积＝×AD×EN＝（5﹣BD）（+BD）＝﹣（BD﹣）2+，

∴当BD＝时，△ADE面积最大值为．