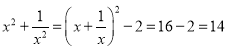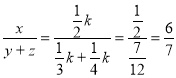Question

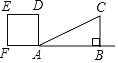
【题目】如图，AB是⊙O的直径，点C在⊙O上，点D在AB的延长线上，且∠BCD∠A．

(1)求证：CD是⊙O的切线；

(2)若AC2，ABCD，求⊙O半径．

Answer 1

【答案】(1)见解析；(2)

【解析】

（1）连接OC．因为AB是⊙O的直径，C是⊙O上一点，可求得∠ACB=90°，因为OA=OC，∠BCD=∠A，可得∠ACO=∠A=∠BCD，易得∠OCD=90°，即CD是⊙O的切线．

（2）设CD为x，分别表示出AB和OC的长度，由勾股定理可求得OD=x,所以BD=OD﹣OB= x，易证△ADC∽△CDB，利用相似三角形的性质求得CB=1，利用勾股定理求出，可得半径为.

(1)证明：如图，连接OC．

∵AB是⊙O的直径，C是⊙O上一点，

∴∠ACB=90°，即∠ACO+∠OCB=90°．

∵OA=OC，∠BCD=∠A，

∴∠ACO=∠A=∠BCD，

∴∠BCD+∠OCB=90°，即∠OCD=90°，

∴CD是⊙O的切线．

(2)解：设CD为x，

则AB=x，OC=OB=x，

∵∠OCD=90°，

∴OD=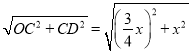=x，

∴BD=OD﹣OB=x﹣x=x，

∵∠BCD＝∠A，∠BDC＝∠CDA，

∴△ADC∽△CDB，

∴，

即，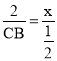

解得CB=1，

∴AB=

∴⊙O半径是．