题目内容
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.
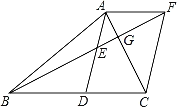
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,①试判断四边形ADCF的形状,并证明你的结论;
②若AB=8,BD=5,直接写出线段AG的长 .
【答案】(1)详见解析;(2)①四边形ADCF是菱形;详见解析;②2
【解析】
(1)由平行线证明三角形全等所缺少的条件,再根据三角形全等的判定方法证明三角形全等;
(2)①先证四边形ADCF是平行四边形,再证明邻边相等,便可得出结论;
②证明△AFG∽△CBG,得出AG与AC的比例关系,进而由直角三角形的性质求得AC,便可得AG.
(1)∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
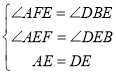 ,
,
∴△AEF≌△DEB(AAS);
(2)①四边形ADCF是菱形,
理由如下:∵△AEF≌△DEB,
∴AF=BD,
∵BD=DC,
∴AF=DC=![]() BC,
BC,
又AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,AD是BC边上的中线,
∴AD=DC,
∴四边形ADCF是菱形;
②∵AF∥BC,
∴△AFG∽△CBG,
∴![]()
∴![]()
∴AG=![]() ,
,
∵BD=5,AD是BC边上的中线,
∴BC=2BD=10,
∵∠BAC=90°,AB=8,
∴AC=![]() ,
,
∴AG=![]() =2,
=2,
故答案为2.

练习册系列答案
相关题目